CD3 - Lagrangianen
Recall: Newtons lag för en partikel med position X(t) och massa 1 i en potential V(x) kan skrivas som:
=-V'(X(t)) "X''(t)=-V'(X(t))")
Lagrangianmetoden går ut på att definiera en "Lagrangian" som beskriver krafterna som verkar på partikeln, och använda denna för att härleda ekvationer för hur partikeln rör sig. I det enklaste fallet är det bara ett krångligare sätt att komma fram till Newtons lag, men denna metod är bättre på att hantera variabelbyten och begränsningar, och om man använder sig av mer exotiska Lagrangianer kan man också beräkna exempelvis partikelbanor kring svarta hål eller i elektromagnetiska fält.
Definitioner
Lagrangianen definieras som följer:
=\tfrac12v^2-V(x) "L(x,v)=\tfrac12v^2-V(x)")
Lagrangianen tilldelar alltså till varje punkt (x,v) i fasrymden ett värde som är differensen mellan rörelseenergi och lägesenergi hos partikeln när den befinner sig i position x med hastighet v.
Vi definerar sedan partikelns verkan (action) längs banan X(t) mellan tidpunkterna a och b som:
,X'(t))\,dt "S[X]=\int_a^bL(X(t),X'(t))\,dt")
Verkan är alltså totala skillnaden mellan rörelseenergi och lägesenergi längs banan. Notera att verkan inte är en funktion av ett numeriskt värde X, utan av en hel funktion X(t). Hakparenteserna används för att påminna om detta.
Rörelseekvationen
Vi postulerar att partikeln följer den bana som maximerar verkan, givet dess start- och slutpunkt.
Det visar sig att denna regel är (typ) ekvivalent med Newtons lag. Vi hittar banan X(t) som maximerar S[X] genom att derivera S med avseende på X och sätta derivatan till 0. Detta är dock ingen vanlig derivata eftersom X är en funktion och inte bara en variabel, så resultatet blir Euler-Lagranges ekvationer:
,X'(t))\right)=\frac{\partial L}{\partial x}(X(t),X'(t)) "\frac d{dt}\left(\frac{\partial L}{\partial v}(X(t),X'(t))\right)=\frac{\partial L}{\partial x}(X(t),X'(t))")
Sätter vi in vårt uttryck för Lagrangianen ovan, får vi tillbaks Newtons lag:
)=-V'(X(t)) "\tfrac d{dt}(X'(t))=-V'(X(t))")
Variabelbyte
Fördelen med att använda Lagrangianen är att postulatet som vi härledde rörelseekvationen ifrån är enkelt att tolka oavsett koordinatsystem. Tag till exempel problemet med att analysera en pendel som kan röra sig i alla tre dimensioner:
Det är naturligt att använda polära rymdkoordinater här, eftersom en av koordinaterna, avståndet från upphängningspunkten, då blir konstant. Istället för att försöka skriva om Newtons lag till polära rymdkoordinater och krångla med gradienter kan man då bara skriva om Lagrangianen, och sedan ger Euler-Lagranges ekvationer med avseende på vinklarna (var för sig!) rätt ekvation:
=\tfrac{ml^2}{2}(\dot\theta^2+\dot\phi^2\sin^2\theta) + mgl\cos\theta\\ \Rightarrow\left\{\begin{matrix} \tfrac{d}{dt}(ml^2\dot\theta)&=&ml^2\dot\phi^2\sin\theta\cos\theta-mgl\sin\theta\\\tfrac{d}{dt}(ml^2\dot\phi\sin^2\theta)&=&0\end{matrix}\right. "L(\theta,\phi,\dot\theta,\dot\phi)=\tfrac{ml^2}{2}(\dot\theta^2+\dot\phi^2\sin^2\theta) + mgl\cos\theta\\ \Rightarrow\left\{\begin{matrix} \tfrac{d}{dt}(ml^2\dot\theta)&=&ml^2\dot\phi^2\sin\theta\cos\theta-mgl\sin\theta\\\tfrac{d}{dt}(ml^2\dot\phi\sin^2\theta)&=&0\end{matrix}\right.")
Notera att Lagrangianmetoden hanterar begränsningar i fasrymden, i detta fallet att partikeln håller sig en stånglängd från upphängningspunkten, utan att blinka. Med Newtons lagar hade vi behövt ställa upp ekvationer för att räkna ut hur stor kraften i stången är och hur stor inverkan den har.
Noethers satser
Den observante läsaren kan ha noterat att en derivata blev noll i förra exemplet. Detta är innehållet i en av Noethers satser: Om Lagrangianen inte beror uttryckligen på en positionsvariabel x, så är kvantiteten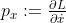
konstant eftersom dess derivata är 0. Denna kvantitet är med standard-Lagrangianen helt enkelt rörelsemängden p=mv i x-riktningen, och kallas därmed generellt för den "konjugerade rörelsemängden" till x.
Noethers lite mer kluriga sats säger att totala "energin" i systemet bevaras (förutom ifall Lagrangianen uttryckligen beror på tiden). Med "energi" menas här inte nödvändigtvis den fysikaliska kvantiteten, men i fallet med standard-Lagrangianen blir det:
 "H = \tfrac12v^2+V(x)")
vilket är just rörelseenergi plus lägesenergi.
Den totala energin H kallas för Hamiltonianen, och ger upphov till ytterligare en metod att beskriva krafterna i ett system för att kunna härleda rörelseekvationerna/Newtons lag.
Lagrangianmetoden går ut på att definiera en "Lagrangian" som beskriver krafterna som verkar på partikeln, och använda denna för att härleda ekvationer för hur partikeln rör sig. I det enklaste fallet är det bara ett krångligare sätt att komma fram till Newtons lag, men denna metod är bättre på att hantera variabelbyten och begränsningar, och om man använder sig av mer exotiska Lagrangianer kan man också beräkna exempelvis partikelbanor kring svarta hål eller i elektromagnetiska fält.
Definitioner
Lagrangianen definieras som följer:
Lagrangianen tilldelar alltså till varje punkt (x,v) i fasrymden ett värde som är differensen mellan rörelseenergi och lägesenergi hos partikeln när den befinner sig i position x med hastighet v.
Vi definerar sedan partikelns verkan (action) längs banan X(t) mellan tidpunkterna a och b som:
Verkan är alltså totala skillnaden mellan rörelseenergi och lägesenergi längs banan. Notera att verkan inte är en funktion av ett numeriskt värde X, utan av en hel funktion X(t). Hakparenteserna används för att påminna om detta.
Rörelseekvationen
Vi postulerar att partikeln följer den bana som maximerar verkan, givet dess start- och slutpunkt.
Det visar sig att denna regel är (typ) ekvivalent med Newtons lag. Vi hittar banan X(t) som maximerar S[X] genom att derivera S med avseende på X och sätta derivatan till 0. Detta är dock ingen vanlig derivata eftersom X är en funktion och inte bara en variabel, så resultatet blir Euler-Lagranges ekvationer:
Sätter vi in vårt uttryck för Lagrangianen ovan, får vi tillbaks Newtons lag:
Variabelbyte
Fördelen med att använda Lagrangianen är att postulatet som vi härledde rörelseekvationen ifrån är enkelt att tolka oavsett koordinatsystem. Tag till exempel problemet med att analysera en pendel som kan röra sig i alla tre dimensioner:
Det är naturligt att använda polära rymdkoordinater här, eftersom en av koordinaterna, avståndet från upphängningspunkten, då blir konstant. Istället för att försöka skriva om Newtons lag till polära rymdkoordinater och krångla med gradienter kan man då bara skriva om Lagrangianen, och sedan ger Euler-Lagranges ekvationer med avseende på vinklarna (var för sig!) rätt ekvation:
Notera att Lagrangianmetoden hanterar begränsningar i fasrymden, i detta fallet att partikeln håller sig en stånglängd från upphängningspunkten, utan att blinka. Med Newtons lagar hade vi behövt ställa upp ekvationer för att räkna ut hur stor kraften i stången är och hur stor inverkan den har.
Noethers satser
Den observante läsaren kan ha noterat att en derivata blev noll i förra exemplet. Detta är innehållet i en av Noethers satser: Om Lagrangianen inte beror uttryckligen på en positionsvariabel x, så är kvantiteten
Noethers lite mer kluriga sats säger att totala "energin" i systemet bevaras (förutom ifall Lagrangianen uttryckligen beror på tiden). Med "energi" menas här inte nödvändigtvis den fysikaliska kvantiteten, men i fallet med standard-Lagrangianen blir det:
vilket är just rörelseenergi plus lägesenergi.
Den totala energin H kallas för Hamiltonianen, och ger upphov till ytterligare en metod att beskriva krafterna i ett system för att kunna härleda rörelseekvationerna/Newtons lag.
Kommentarer