CD4 - Hamiltonianen
Recall: Newtons lag för en partikel med position X(t) i en potential V(x) kan skrivas som:
=-V'(X(t)))
där P(t) := mX'(t) är partikelns rörelsemängd.
Hamiltonianmetoden är precis som Lagrangianmetoden ett alternativ till Newtons lagar. Personligen tycker jag att denna metod inte är särskilt användbar - medan Lagrangianen förenklar vissar saker krånglar Hamiltonianen mest bara till dem. Dock visar det sig att Hamiltonianen utgör grunden för kvantmekanik, till skillnad från Newtons lagar eller Lagrangianen.
Definition
Standard-Hamiltonianen för en partikel med position x och rörelsemängd p är:
=\tfrac{p^2}{2m}+V(x))
Detta är helt enkelt rörelseenergi + lägesenergi, dvs partikelns totala energi.
Hamiltons ekvationer är:
=-\frac{\partial H}{\partial x}(X(t),P(t)),\quad X'(t)=\frac{\partial H}{\partial p}(X(t),P(t)))
Notera att dessa ekvationer är nästan helt symmetriska i p och x, sånär som på ett litet minustecken. Finns det någon anledning till att ekvationerna ska se ut just såhär? Jag känner inte till någon, förutom det faktum att det stämmer, vilket vi kan kontrollera genom att sätta in uttrycket för H ovan:
)=P'(t),\quad\tfrac{\partial H}{\partial p}=\tfrac{P(t)}{m}=X'(t))
Konservation
Som jag nämnt tidigare är Hamiltonianen, som tolkas som totala energin, konstant. Detta visas lätt med kedjeregeln och Hamiltons ekvationer:
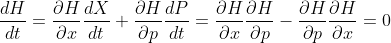
Detta underlättar analys av systemet, eftersom det ger en ekvation som kan användas för att eliminera en av de obekanta variablerna.
Exempel
Det klassiska Hamiltonian-exemplet är den harmoniska oscillatorn med Hamiltonianen:
=\tfrac{p^2}{2m}+\tfrac{1}{2}m\omega^2x^2)
Potentialen är alltså på formen V(x)=kx2, och kraften F=-V'(x)=-kx. I skolan brukar man se denna modell för en tyngd i en fjäder eller möjligen en pendel, men faktum är att många fysikaliska system kan approximeras som en harmonisk oscillator.
För vidare analys kan vi ignorera det oväsentliga och förenkla Hamiltonianen till:
=\tfrac{1}{2}(p^2+x^2))
Tack vare konservation kan vi då utan att lösa några differentialekvationer redan säga en sak om systemet: dess bana i fasrymden är en cirkel (egentligen en ellips) x2+p2 = konstant.
Hamiltons ekvationer:
=P(t),\quad P'(t)=-X(t)\\ \Rightarrow X''(t)=P'(t)=-X(t)\\ \Rightarrow X(t)=A\sin(t-t_0),\quad P(t)=A\cos(t-t_0))
Partikeln färdas alltså längs cirkeln i fasrymden med jämn hastighet. (Här gick det bra att lösa ekvationerna utan att använda att H är konstant, men så är ofta inte fallet.) Notera att detta är ett exempel där Hamiltonian-metoden inte förenklar något: om vi hade använt Newtons ekvation hade vi fått x''(t) = -x(t) direkt.
där P(t) := mX'(t) är partikelns rörelsemängd.
Hamiltonianmetoden är precis som Lagrangianmetoden ett alternativ till Newtons lagar. Personligen tycker jag att denna metod inte är särskilt användbar - medan Lagrangianen förenklar vissar saker krånglar Hamiltonianen mest bara till dem. Dock visar det sig att Hamiltonianen utgör grunden för kvantmekanik, till skillnad från Newtons lagar eller Lagrangianen.
Definition
Standard-Hamiltonianen för en partikel med position x och rörelsemängd p är:
Detta är helt enkelt rörelseenergi + lägesenergi, dvs partikelns totala energi.
Hamiltons ekvationer är:
Notera att dessa ekvationer är nästan helt symmetriska i p och x, sånär som på ett litet minustecken. Finns det någon anledning till att ekvationerna ska se ut just såhär? Jag känner inte till någon, förutom det faktum att det stämmer, vilket vi kan kontrollera genom att sätta in uttrycket för H ovan:
Konservation
Som jag nämnt tidigare är Hamiltonianen, som tolkas som totala energin, konstant. Detta visas lätt med kedjeregeln och Hamiltons ekvationer:
Detta underlättar analys av systemet, eftersom det ger en ekvation som kan användas för att eliminera en av de obekanta variablerna.
Exempel
Det klassiska Hamiltonian-exemplet är den harmoniska oscillatorn med Hamiltonianen:
Potentialen är alltså på formen V(x)=kx2, och kraften F=-V'(x)=-kx. I skolan brukar man se denna modell för en tyngd i en fjäder eller möjligen en pendel, men faktum är att många fysikaliska system kan approximeras som en harmonisk oscillator.
För vidare analys kan vi ignorera det oväsentliga och förenkla Hamiltonianen till:
Tack vare konservation kan vi då utan att lösa några differentialekvationer redan säga en sak om systemet: dess bana i fasrymden är en cirkel (egentligen en ellips) x2+p2 = konstant.
Hamiltons ekvationer:
Partikeln färdas alltså längs cirkeln i fasrymden med jämn hastighet. (Här gick det bra att lösa ekvationerna utan att använda att H är konstant, men så är ofta inte fallet.) Notera att detta är ett exempel där Hamiltonian-metoden inte förenklar något: om vi hade använt Newtons ekvation hade vi fått x''(t) = -x(t) direkt.
Kommentarer
