DS1 - Fasrymder och kaos
Dynamical Systems handlar om:
* Fixpunkter
* Stabilitet
* Periodiska banor
* Bifurkationer
* Kaos
Allt intressant i denna kurs kommer sammanfattas i detta inlägg.
Dynamiska system
Med ett dynamiskt system menar jag en samling variabler som förändras med tiden efter en bestämd regel. I denna kurs behandlar vi dynamiska system av två typer:
* Kontinuerliga, som beskrivs av x'(t) = f(x(t)).
* Diskreta, som beskrivs av x(n+1) = g(x(n)).
Ett tråkigt exempel på ett diskret dynamiskt system är obegränsad befolkningstillväxt: Om x(n) är populationen efter n år, fås ekvationen x(n+1) = k·x(n), där k är en konstant.
Den logistiska ekvationen x(n+1) = k·x(n)·(A - x(n)) är en modell för befolkningstillväxt när området bara kan upprätthålla en begränsad population.
Ett exempel på ett kontinuerligt dynamiskt system är hastigheten hos en fallande partikel med luftmotstånd: v'(t) = g - kv(t)^2/m.
Det klassiska exemplet på ett kontinuerligt system är en tyngd i en fjäder, som beskrivs av elongationen x(t) från jämviktsläget och hastigheten v(t). Ekvationerna lyder x'(t) = v(t), v'(t) = -k·x(t). Här är en bild:
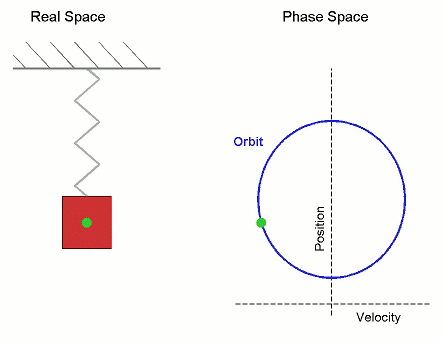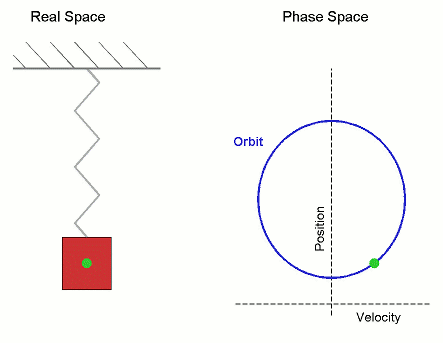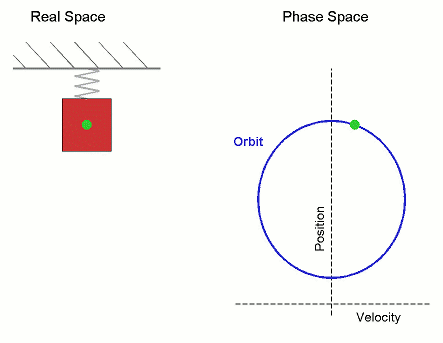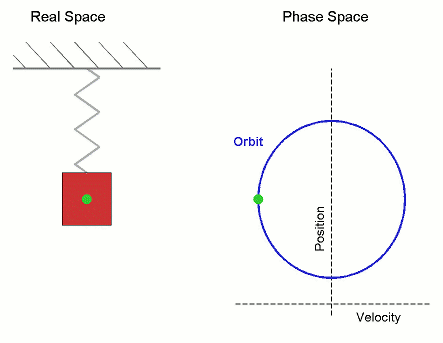
Fasrymden
Precis som den högra delen av ovanstående bild visar, tänker vi oss att variablerna i det dynamiska systemet är koordinater för en punkt i en lämplig rymd, fasrymden. I exemplet hade vi hastighet och position, som tolkas som x- och y-koordinat i planet. (Nu finner vi Wikipedias definition av ett dynamiskt system: En regel som beskriver hur en punkt i någon rymd förflyttas med tiden.)
I både det diskreta och det kontinuerliga fallet kan vi tala om banor (trajectories): Hur systemet utvecklas från en viss punkt. I det kontinuerliga fallet är detta en kurva i fasrymden (såsom cirkeln ovan), medan det i det diskreta fallet blir en sekvens av punkter.
Huvudpoängen i denna kurs är att bilda sig uppfattningar om hur banorna ser ut i fasrymden.
Den stora skillnaden på fasrymden och vanliga rymden, är att positionen i fasrymden fullständigt beskriver systemets tillstånd: För att beskriva en partikel i 3 dimensioner använder vi en sexdimensionell fasrymd - tre dimensioner för positionen, och tre för hastigheten.
Att systemet är fullständigt bestämt utifrån punktens position ger en viktig regel: Trajectories do not cross!. Om två banor möts i en punkt, så måste de fortsätta tillsammans, eftersom de följer exakt samma utvecklingsregler från denna punkt. I det kontinuerliga fallet kan man vanligtvis även köra systemet baklänges, så man kan rita fullständiga banor både framåt och bakåt i tiden från en given punkt. I det diskreta fallet är det vanligt att olika banor möts och fortsätter tillsammans, så när man spolar bandet baklänges blir det en massa förgreningar.
Regeln att banor inte korsas är viktig för kontinuerliga 2D-system, eftersom det begränsar möjligheterna drastiskt (till skillnad från i högre dimensioner där det är jättelätt att rita komplicerade figurer, exempelvis knutar, med kurvor som inte korsar varandra). Det är därför det krävs minst tre dimensioner för att ett kontinuerligt system ska kunna uppvisa kaotiskt beteende (se nedan).
Stabilitet
Den enklaste typen av bana är en fix punkt x0. Den uppfyller
* f(x0) = 0 för kontinuerliga system, så att x'(t) = 0.
* g(x0) = x0 för diskreta system, så att x(n+1) = x(n).
En intressant fråga är huruvida fixpunkten är stabil, dvs om systemet rubbas litegrann och istället följer banan x(t) = x0 + δ(t), där δ(t) är litet till att börja med, hur kommer det då utveckla sig? Det visar sig (genom Taylorutveckling) att perturbationen δ(t) oftast ökar eller minskar exponentiellt, motsvarande att punkten är instabil eller stabil.
En annan sorts bana är periodiska banor (dvs banor som upprepar sig), exempelvis den som systemet i bilden ovan följer. Här kan man också analysera stabilitet.
Stabilitet är en viktig fråga, eftersom det är främst de stabila tillstånden man finner i den verkliga världen. Exempelvis är det en försvinnande liten andel av alla pennor i världen som just nu balanserar på sin spets.
Kaos
Kaos är idén att en fjärils vingslag kan orsaka en orkan på andra sidan jordklotet.
Denna idé är relaterad till det första kriteriet i definitionen av ett kaotiskt system: Sensitive dependence on initial conditions (SDIC). Detta innebär att små skillnader i utgångspunkt (exempelvis en fjärils vingslag) för det dynamiska systemet kan växa till jättestora skillnader (exempelvis en orkan).
Ursprungligen upptäcktes kaotiska system när man försökte förutspå vädret med hjälp av datorberäkningar. Någon hade låtit en dator göra en längre beräkning, och när denne startade om beräkningen från mitten med hjälp av de delresultat datorn hade skrivit ut blev slutresultatet helt annorlunda. Det berodde på att de utskrivna delresultaten var avrundade, och vid omkörningen växte de små avrundningsfelen genom SDIC och "förstörde" beräkningen.
Det är "på grund av" kaos som vi idag inte kan förutspå vädret mer än ungefär en vecka framåt i tiden: Går man längre blir felen från vädermodellens och mätvärdenas inexakthet för stora.
Notera att kaos uppstår trots att systemet är helt deterministiskt, dvs att det inte finns någon slump inblandad. Att slutresultatet ser slumpmässigt ut beror just på SDIC: I början mäter vi på systemet och finner att det befinner sig någonstans i ett litet område (som inte är en enda punkt på grund av mätosäkerheten). När vi spolar tiden framåt växer detta område och sprider ut sig över hela fasrymden. Vart systemet faktiskt tar vägen förefaller slumpmässigt.
Det andra kriteriet för kaos är Topological Transitivity (TT), vilket betyder att vilka två områden man än tänker på så finns det en bana som går från den ena till den andra. Detta utesluter tråkiga SDIC-system, såsom simpel exponentiell tillväxt (där det är uppenbart att små skillnader växer sig stora).
De två kriterierna för kaos kan alltså sammanfattas som "små skillnader kan explodera" och "banor blandas om". Ett exempel på ett kaotiskt system är dubbelpendeln: En pendel som det sitter en pendel på. Wikipedia har en bild på systemet:

och en exempelkörning (fast inte i den fyrdimensionella fasrymden, utan bara den tvådimensionella positionsrymden):

Att skriva om differentialekvationer till önskad form
Längst upp i detta inlägg definierade jag kontinuerliga system som x'(t) = f(x(t)), vilket är ett autonomt system av differentialekvationer av första ordningen. Det visar sig att många fler differentialekvationer kan skrivas på denna form, med hjälp av två trick.
Ett av dem har vi redan sett, nämligen hur man minskar ordningen av en ekvation genom att införa fler variabler. (Detta är användbart för MATLAB-användare, då MATLAB endast löser första ordningens diffekvationer.) Som jag nämnt i tidigare inlägg beskrivs ju fysiken för en partikel vanligtvis genom en andra ordningens diffekvation x''(t) = F(x'(t), x(t)). Genom att införa hastigheten v(t) = x'(t) som egen variabel blir den nya obekanta en tvådimensionell vektor (x(t), v(t)) som uppfyller diffekvationssystemet (x'(t), v'(t)) = f(x(t), v(t)) = (v(t), F(v(t), x(t))). Generellt, för att minska med k ordningar så behövs k nya variabler.
Det andra tricket är att omvandla ett icke-autonomt system (där regeln förändras med tiden) till ett autonomt system (där regeln inte beror på tiden), vilket exempelvis är användbart om man studerar sin pendel ombord på ett kapsejsande skepp. Detta löses genom att man inför tiden som egen variabel, T(t) = t. Istället för x'(t) = F(x(t), t) blir det (x'(t), T'(t)) = f(x(t), T(t)) = (F(x(t), T(t)), 1).
Andra exempel (bonuskapitel)
Pendel (på stång): Denna pendels position kan beskrivas med vinkeln mot lodlinjen, och som hastighet tar vi då tidsderivatan av vinkeln. Eftersom 0° rotation är samma som 360° rotation, blir fasrymden inte ett plan, utan en cylinder: Om man går 360° i positionsriktningen kommer man tillbaks till där man startade, men man kan gå godtyckligt långt i hastighetsriktningen utan att komma tillbaks (alla hastigheter är genuint olika).
Banorna ser ut såhär:

Bilden ska rullas ihop vertikalt, så att vänstra och högra kanten klistras ihop. I mitten finns vanliga oscillationer (libration), runt en stabil fixpunkt. Den fixpunkt som befinner sig längst till både höger och vänster i mitten är den där pendeln befinner sig rakt ovanför axeln, vilket självklart är instabilt. Längst uppe och nere är de tillstånd då pendeln har så hög fart att den bara snurrar runt åt ena hållet (rotation). De rödmarkerade banorna kallas separatriser, och är gränsen mellan libration och rotation. Där har pendeln lika mycket total energi som i den instabila fixpunkten, och systemet behöver oändlig tid på sig att nå denna punkt längs separatrisen.
Pendeln är ett specialfall av en generell klass av 2D-system kallade Hamiltonska system. Dessa kännetecknas av att man kan definiera en Hamiltonian H(x,y) (som måste uppfylla x' = dH/dy, y' = -dH/dx). Hamiltonianen tolkas som totala energin i systemet, eftersom det är just vad det är för exempelvis tyngden i fjädern ovan. (Mer om detta i CD).
Eftersom systemet följer banor med konstant Hamiltonian, blir det mycket lätt att analysera. Det är bara att rita nivåkurvorna (H = konstant) för Hamiltonianen, så har man systemets banor.
En lite svårare, men ändå relativt lätt, klass av system är nästan-Hamiltonska system. Detta är system som skiljer sig väldigt lite från Hamiltonska flöden, och analyseras genom att man studerar hur Hamiltonianen (för det snarlika Hamiltonska systemet) förändras längs banorna i detta nya system.
Exempelvis kan vi ta pendeln ovan, fast med någon sorts dämpning, säg luftmotstånd, i enkel svängning (libration). Utan luftmotstånd hade den svängt så för evigt, men nu förlorar den långsamt energi. Att lösa diffekvationssystemet fullständigt skulle vara svårt, men när luftmotståndet är svagt gör vi en approximation som följer: Vi antar att pendeln under en svängning följer den friktionsfria banan, men räknar ut hur mycket energi den skulle förlora om det fanns luftmotstånd. När svängningen är klar drar vi av denna energi, och räknar på nästa svängning på den nya, lägre, energinivån.
Denna metod kommer ge ett litet fel, eftersom pendeln egentligen saktar in kontinuerligt. Under varje svängning överskattar vi pendelns hastighet (och därmed luftmotståndet) när vi säger att den följer den friktionsfria banan genom fasrymden, så denna approximation ger antagligen en för snabb inbromsning (om inte andra faktorer spelar in). Felet är dock litet om luftmotståndet är litet.
* Fixpunkter
* Stabilitet
* Periodiska banor
* Bifurkationer
* Kaos
Allt intressant i denna kurs kommer sammanfattas i detta inlägg.
Dynamiska system
Med ett dynamiskt system menar jag en samling variabler som förändras med tiden efter en bestämd regel. I denna kurs behandlar vi dynamiska system av två typer:
* Kontinuerliga, som beskrivs av x'(t) = f(x(t)).
* Diskreta, som beskrivs av x(n+1) = g(x(n)).
Ett tråkigt exempel på ett diskret dynamiskt system är obegränsad befolkningstillväxt: Om x(n) är populationen efter n år, fås ekvationen x(n+1) = k·x(n), där k är en konstant.
Den logistiska ekvationen x(n+1) = k·x(n)·(A - x(n)) är en modell för befolkningstillväxt när området bara kan upprätthålla en begränsad population.
Ett exempel på ett kontinuerligt dynamiskt system är hastigheten hos en fallande partikel med luftmotstånd: v'(t) = g - kv(t)^2/m.
Det klassiska exemplet på ett kontinuerligt system är en tyngd i en fjäder, som beskrivs av elongationen x(t) från jämviktsläget och hastigheten v(t). Ekvationerna lyder x'(t) = v(t), v'(t) = -k·x(t). Här är en bild:

Fasrymden
Precis som den högra delen av ovanstående bild visar, tänker vi oss att variablerna i det dynamiska systemet är koordinater för en punkt i en lämplig rymd, fasrymden. I exemplet hade vi hastighet och position, som tolkas som x- och y-koordinat i planet. (Nu finner vi Wikipedias definition av ett dynamiskt system: En regel som beskriver hur en punkt i någon rymd förflyttas med tiden.)
I både det diskreta och det kontinuerliga fallet kan vi tala om banor (trajectories): Hur systemet utvecklas från en viss punkt. I det kontinuerliga fallet är detta en kurva i fasrymden (såsom cirkeln ovan), medan det i det diskreta fallet blir en sekvens av punkter.
Huvudpoängen i denna kurs är att bilda sig uppfattningar om hur banorna ser ut i fasrymden.
Den stora skillnaden på fasrymden och vanliga rymden, är att positionen i fasrymden fullständigt beskriver systemets tillstånd: För att beskriva en partikel i 3 dimensioner använder vi en sexdimensionell fasrymd - tre dimensioner för positionen, och tre för hastigheten.
Att systemet är fullständigt bestämt utifrån punktens position ger en viktig regel: Trajectories do not cross!. Om två banor möts i en punkt, så måste de fortsätta tillsammans, eftersom de följer exakt samma utvecklingsregler från denna punkt. I det kontinuerliga fallet kan man vanligtvis även köra systemet baklänges, så man kan rita fullständiga banor både framåt och bakåt i tiden från en given punkt. I det diskreta fallet är det vanligt att olika banor möts och fortsätter tillsammans, så när man spolar bandet baklänges blir det en massa förgreningar.
Regeln att banor inte korsas är viktig för kontinuerliga 2D-system, eftersom det begränsar möjligheterna drastiskt (till skillnad från i högre dimensioner där det är jättelätt att rita komplicerade figurer, exempelvis knutar, med kurvor som inte korsar varandra). Det är därför det krävs minst tre dimensioner för att ett kontinuerligt system ska kunna uppvisa kaotiskt beteende (se nedan).
Stabilitet
Den enklaste typen av bana är en fix punkt x0. Den uppfyller
* f(x0) = 0 för kontinuerliga system, så att x'(t) = 0.
* g(x0) = x0 för diskreta system, så att x(n+1) = x(n).
En intressant fråga är huruvida fixpunkten är stabil, dvs om systemet rubbas litegrann och istället följer banan x(t) = x0 + δ(t), där δ(t) är litet till att börja med, hur kommer det då utveckla sig? Det visar sig (genom Taylorutveckling) att perturbationen δ(t) oftast ökar eller minskar exponentiellt, motsvarande att punkten är instabil eller stabil.
En annan sorts bana är periodiska banor (dvs banor som upprepar sig), exempelvis den som systemet i bilden ovan följer. Här kan man också analysera stabilitet.
Stabilitet är en viktig fråga, eftersom det är främst de stabila tillstånden man finner i den verkliga världen. Exempelvis är det en försvinnande liten andel av alla pennor i världen som just nu balanserar på sin spets.
Kaos
Kaos är idén att en fjärils vingslag kan orsaka en orkan på andra sidan jordklotet.
Denna idé är relaterad till det första kriteriet i definitionen av ett kaotiskt system: Sensitive dependence on initial conditions (SDIC). Detta innebär att små skillnader i utgångspunkt (exempelvis en fjärils vingslag) för det dynamiska systemet kan växa till jättestora skillnader (exempelvis en orkan).
Ursprungligen upptäcktes kaotiska system när man försökte förutspå vädret med hjälp av datorberäkningar. Någon hade låtit en dator göra en längre beräkning, och när denne startade om beräkningen från mitten med hjälp av de delresultat datorn hade skrivit ut blev slutresultatet helt annorlunda. Det berodde på att de utskrivna delresultaten var avrundade, och vid omkörningen växte de små avrundningsfelen genom SDIC och "förstörde" beräkningen.
Det är "på grund av" kaos som vi idag inte kan förutspå vädret mer än ungefär en vecka framåt i tiden: Går man längre blir felen från vädermodellens och mätvärdenas inexakthet för stora.
Notera att kaos uppstår trots att systemet är helt deterministiskt, dvs att det inte finns någon slump inblandad. Att slutresultatet ser slumpmässigt ut beror just på SDIC: I början mäter vi på systemet och finner att det befinner sig någonstans i ett litet område (som inte är en enda punkt på grund av mätosäkerheten). När vi spolar tiden framåt växer detta område och sprider ut sig över hela fasrymden. Vart systemet faktiskt tar vägen förefaller slumpmässigt.
Det andra kriteriet för kaos är Topological Transitivity (TT), vilket betyder att vilka två områden man än tänker på så finns det en bana som går från den ena till den andra. Detta utesluter tråkiga SDIC-system, såsom simpel exponentiell tillväxt (där det är uppenbart att små skillnader växer sig stora).
De två kriterierna för kaos kan alltså sammanfattas som "små skillnader kan explodera" och "banor blandas om". Ett exempel på ett kaotiskt system är dubbelpendeln: En pendel som det sitter en pendel på. Wikipedia har en bild på systemet:
och en exempelkörning (fast inte i den fyrdimensionella fasrymden, utan bara den tvådimensionella positionsrymden):

Att skriva om differentialekvationer till önskad form
Längst upp i detta inlägg definierade jag kontinuerliga system som x'(t) = f(x(t)), vilket är ett autonomt system av differentialekvationer av första ordningen. Det visar sig att många fler differentialekvationer kan skrivas på denna form, med hjälp av två trick.
Ett av dem har vi redan sett, nämligen hur man minskar ordningen av en ekvation genom att införa fler variabler. (Detta är användbart för MATLAB-användare, då MATLAB endast löser första ordningens diffekvationer.) Som jag nämnt i tidigare inlägg beskrivs ju fysiken för en partikel vanligtvis genom en andra ordningens diffekvation x''(t) = F(x'(t), x(t)). Genom att införa hastigheten v(t) = x'(t) som egen variabel blir den nya obekanta en tvådimensionell vektor (x(t), v(t)) som uppfyller diffekvationssystemet (x'(t), v'(t)) = f(x(t), v(t)) = (v(t), F(v(t), x(t))). Generellt, för att minska med k ordningar så behövs k nya variabler.
Det andra tricket är att omvandla ett icke-autonomt system (där regeln förändras med tiden) till ett autonomt system (där regeln inte beror på tiden), vilket exempelvis är användbart om man studerar sin pendel ombord på ett kapsejsande skepp. Detta löses genom att man inför tiden som egen variabel, T(t) = t. Istället för x'(t) = F(x(t), t) blir det (x'(t), T'(t)) = f(x(t), T(t)) = (F(x(t), T(t)), 1).
Andra exempel (bonuskapitel)
Pendel (på stång): Denna pendels position kan beskrivas med vinkeln mot lodlinjen, och som hastighet tar vi då tidsderivatan av vinkeln. Eftersom 0° rotation är samma som 360° rotation, blir fasrymden inte ett plan, utan en cylinder: Om man går 360° i positionsriktningen kommer man tillbaks till där man startade, men man kan gå godtyckligt långt i hastighetsriktningen utan att komma tillbaks (alla hastigheter är genuint olika).
Banorna ser ut såhär:

Bilden ska rullas ihop vertikalt, så att vänstra och högra kanten klistras ihop. I mitten finns vanliga oscillationer (libration), runt en stabil fixpunkt. Den fixpunkt som befinner sig längst till både höger och vänster i mitten är den där pendeln befinner sig rakt ovanför axeln, vilket självklart är instabilt. Längst uppe och nere är de tillstånd då pendeln har så hög fart att den bara snurrar runt åt ena hållet (rotation). De rödmarkerade banorna kallas separatriser, och är gränsen mellan libration och rotation. Där har pendeln lika mycket total energi som i den instabila fixpunkten, och systemet behöver oändlig tid på sig att nå denna punkt längs separatrisen.
Pendeln är ett specialfall av en generell klass av 2D-system kallade Hamiltonska system. Dessa kännetecknas av att man kan definiera en Hamiltonian H(x,y) (som måste uppfylla x' = dH/dy, y' = -dH/dx). Hamiltonianen tolkas som totala energin i systemet, eftersom det är just vad det är för exempelvis tyngden i fjädern ovan. (Mer om detta i CD).
Eftersom systemet följer banor med konstant Hamiltonian, blir det mycket lätt att analysera. Det är bara att rita nivåkurvorna (H = konstant) för Hamiltonianen, så har man systemets banor.
En lite svårare, men ändå relativt lätt, klass av system är nästan-Hamiltonska system. Detta är system som skiljer sig väldigt lite från Hamiltonska flöden, och analyseras genom att man studerar hur Hamiltonianen (för det snarlika Hamiltonska systemet) förändras längs banorna i detta nya system.
Exempelvis kan vi ta pendeln ovan, fast med någon sorts dämpning, säg luftmotstånd, i enkel svängning (libration). Utan luftmotstånd hade den svängt så för evigt, men nu förlorar den långsamt energi. Att lösa diffekvationssystemet fullständigt skulle vara svårt, men när luftmotståndet är svagt gör vi en approximation som följer: Vi antar att pendeln under en svängning följer den friktionsfria banan, men räknar ut hur mycket energi den skulle förlora om det fanns luftmotstånd. När svängningen är klar drar vi av denna energi, och räknar på nästa svängning på den nya, lägre, energinivån.
Denna metod kommer ge ett litet fel, eftersom pendeln egentligen saktar in kontinuerligt. Under varje svängning överskattar vi pendelns hastighet (och därmed luftmotståndet) när vi säger att den följer den friktionsfria banan genom fasrymden, så denna approximation ger antagligen en för snabb inbromsning (om inte andra faktorer spelar in). Felet är dock litet om luftmotståndet är litet.
Kommentarer
