pelli

Hur stor andel av grafiten i en vanlig blyertspenna hamnar egentligen på papperet? Det finns tre faktorer som gör att grafiten går till spillo:

1. Delar av grafiten vässas bort, särskilt yttersta lagret eftersom spetsen blir för trubbig innan man kommer dit. I min penna är grafitstiftet 2mm i diameter, men när själva spetsen malts ner till att bli 1mm tjock börjar det bli dags att vässa. Därmed använder jag bara 25% av stiftets tvärsnittsarea.

2. Stiftet går av under vässning. Jag vet inte om det är min penna som är dålig, men ungefär var tredje gång jag vässar pennan går en 5mm lång bit av spetsen av. Jag uppskattar att endast 50% av stiftets längd överlever vässningen.

3. Sista biten av pennan är för kort för att användas. Mitt avstånd mellan fingerspetsar och tumveck är 7cm, så när pennan blir kortare än det börjar den vingla. Den som inte vill anstränga sig kastar alltså bort en 18cm-penna efter 60% av dess längd.

Totalt innebär detta att 7.5% av grafitstiftet hamnar på papperet, medan 92.5% hamnar i papperskorgen. Notera dock att jag inte påstår att detta är slöseri - jag har inte analyserat alternativen och kan därmed inte uttala mig om ifall det finns något effektivare sätt (oavsett det är ur privatekonomiskt, samhällsekonomiskt eller environmentalt perspektiv). Jag vet inte ens om det är grafiten eller träet i pennan som kostar mest.

Som jämförelse är stiftet till en stiftpenna 6cm långt. Det börjar bli krångligt när det är 2cm kvar, men om man trixar lite så behöver man bara kasta bort 5mm. Därmed använder man över 90% av grafiten.

(Min erfarenhet är att en 18cm-penna kostar 1kr och att 40 stift kostar £1.16. Med mina siffror kostar då blyertspennan 9 öre per cm stift eller 0.3 öre per mm^3 grafit att använda, medan stiftpennan kostar 5 öre/cm eller 0.7 öre/mm^3. För att få ut användbara siffror måste man sedan räkna på att blyertsstrecken blir olika tjocka, och att detta medför att man skriver olika stora bokstäver, och att detta medför att man använder olika mycket papper.)

Igår, under Asymptotic Methods, satt jag på främsta raden, och när jag vände mig om reagerade jag på att nästan alla på rad två och tre i föreläsningssalen var kineser (bara omkring 3 av de 20 var icke-kineser).

(Tidigare denna termin hade någon jag känner skrivit anställningsprov för GCHQ, Storbritanniens motsvarighet till FRA, och då reagerat på att det var något konstigt med de över 100 medsökande. Senare insåg denne att det var för att det inte fanns en enda kines med - man måste ju vara brittisk medborgare.)

Detta fick mig att tänka efter ifall det kunde finnas en anledning bakom en eventuell korrelation mellan att vara kines och att läsa applied (fast min observation påvisar inte någon sådan korrelation eftersom en femtedel av alla matematiker är kineser, och vi var ungefär 100 personer i rummet).

Mina föräldrar ville att jag skulle läsa applied, för att det skulle ge mig bredare möjligheter i framtiden, men det första jag kom att tänka på nu var den "vanliga" anledningen till att folk väljer applied - det är lättare. Jag kom då att fundera på ifall det är så att kineserna här har sämre studieresultat.

Jag har nyligen hört talas om två kineser i vår årskull som har fått gå om ett år, vilket jag antar är på grund av dåliga studieresultat, men dessa anekdotala bevis är förstås inte att lita på. Därför letade jag fram provresultaten från våra första och andra år, och sorterade ut folk med kinesiskklingande efternamn. Här är resultaten:



Det vänstra diagrammet är resultatet från första året, och det högra är från andra året. Rött (1st class) nere till höger är bäst, och sedan kommer betygen i fallande ordning medurs, till svart (Ordinary) som är sämst. Den inre cirkeln är kinesernas resultat, medan den yttre är ickekinesernas.

Det är uppenbart att vi kineser presterar sämre än övriga populationen, eftersom alla gränser mellan betygsstegen (förutom 1/2.1-gränsen i första året) kommer tidigare för oss, dvs svaret på frågan "var det störst andel av kineserna eller ickekineserna som fick åtminstone betyg X?" är till vår nackdel i 7 av 8 fall. (Dessutom saknas en större andel av kineserna helt från listan i tvåan, något som oftast tyder på avhopp/kursbyte.) Comrades, I am disappoint.

Vad kan det då bero på att kineser (eller rättare sagt de personer som jag tror är kineser baserat på efternamnet) presterar sämre?
* Kan det vara ett simpelt urvalsfel, dvs att kineserna som helhet är lika bra, men fler medelmåttiga kineser lyckas bli antagna och dra ner snittet? Det kanske tvärtom är starkt av oss att 5% av alla matematiker är kineser med högsta betyg, i ett land där mindre än 1% av alla invånare är kineser överhuvudtaget? Notera att kineser utgör ca 20% av världens befolkning, av matematikerna här, och av alla med högsta betyg.
* Har det något med den ökända kinesförälderstereotypen att göra? Kanske har kineserna svårt att plugga om de inte får skäll? Kanske är den hårda pressen generellt dålig för studierna?
* Är det helt enkelt generella invandrarproblem, såsom språksvårigheter eller ovana vid utbildningssystemet?

Notera dock att en stor brist i min statistik är att jag inte kan skilja på folk som har växt upp i och utanför Kina.

Här får du en inblick i hur jag modellerar världen. Om du stöter på ord du inte förstår är det bara att låtsas som att det inte finns och läsa vidare.

Definition. Ett "utfallsrum" U är en (uppräknelig, för enkelhetens skull) mängd utfall tillsammans med en binär relation "inte bättre än" som uppfyller följande:
1) Totalitet: Om a och b är två utfall, så gäller åtminstone ett av "a är inte bättre än b" och "b är inte bättre än a".
2) Transitivitet: Om a,b,c är tre utfall, sådana att a inte är bättre än b, och b inte är bättre än c, ja då är inte heller a bättre än c.

Definition. Om a och b är två utfall sådana att a inte är bättre än b och b inte är bättre än a, då säger vi att a och b är "lika bra".

Den första definitionen håller nog alla med om beskriver de inblandade orden på ett bra sätt. Jag har med flit valt formuleringen "inte bättre än", för att det ska låta uppenbart att alla utfall är jämförbara (vilket jag anser). Någon kanske skulle invända ifall jag påstod att ett av påståendena "a är bättre än b", "a och b är lika bra", eller "b är bättre än a" måste gälla.

Definition. En "sannolikhetsfunktion" p på ett utfallsrum U uppfyller:
1) Sannolikheten p(a) ≥ 0 för alla utfall a.
2) Summan av alla sannolikheter är 1.

Definition. Ett "valalternativ" i ett utfallsrum U är en sannolikhetsfunktion. Ett "val" är en mängd av valalternativ.

Den första definitionen är bara teknisk. Den andra uttrycker exakt vad jag ser ett val som: Man har en mängd alternativ, där varje alternativ har olika sannolikheter att ge olika utfall. Frågan är hur man avgör vilket alternativ som är bäst.

Definition. En "värderingsfunktion" v på ett utfallsrum U är en reell funktion som uppfyller:
* a är inte bättre än b om och endast om v(a) ≤ v(b).

Sats. På varje utfallsrum U kan man definiera en värderingsfunktion.
Bevis. Tilldela utfallen värden ett i taget, med olikheten i åtanke. Detta går alltid att göra. (Detaljerna överlämnas åt läsaren.)

Den första definitionen säger att en värderingsfunktion sätter ett numeriskt värde på alla utfall, och bättre utfall har högre värde. Satsen säger att man alltid kan sätta värden på utfall. Notera dock att jag exempelvis inte har påstått att det är meningsfullt att addera eller subtrahera värden

Exempel. Låt U bestå av talpar (m,n), som tolkas som utfallet att du har m vänner och n kronor på banken. Värderingen "ju fler vänner desto bättre, pengar kommer i andra hand" kan då realiseras genom värderingsfunktionen v(m,n) = 10*m + arctan(n). Denna funktion är växande i både m och n, men v(M,N) > v(m,n) gäller så länge M > m. Det går alltså mycket väl att modellera påståendet "3 vänner är oändligt mycket sämre än att ha 4" (i bemärkelsen att inget annat kan kompensera för den saknade vännen), trots att vi bara använder ändliga tal.

Jag har inte heller påstått att värderingar går att bestämma i praktiken, men det jag är ute efter är en rent teoretisk definition för vilket val som är bäst. Man måste ha en teoretisk definition som mål, innan man kan börja sätta upp praktiska metoder för att göra bästa valet.

Definition. Det "E-bästa" valalternativet i ett val är det som maximerar genomsnittliga värdet av utfallet. Ett utfallsrum U med värderingsfunktion v sägs vara "vettigt" (för person X) om, i alla möjliga val, det E-bästa alternativet är det som (person X finner) är bäst.

Jag har valt att använda "E-bäst" (där E står för expectancy, dvs väntevärde / genomsnitt), eftersom det är enkelt och i viss mån praktiskt. I nästa mening gör jag sedan avsteg från den rigorösa matematiken, genom att dra in folks preferenser. Det är här modelleringen börjar: Givet en utfallsrum U och en person X, kan vi välja en vettig värderingsfunktion v? (Eftersom jag inte har ställt några krav på preferenserna så är detta generellt sett inte möjligt.)

Exempel

Anledningen till att det är praktiskt att använda väntevärde är att det är vad man får med hög sannolikhet om man lägger ihop många försök. Om du exempelvis spelar om småpengar varje dag i ett år, så gör du bäst i att försöka maximera genomsnittsvinsten varje dag, så där kan en vettig modell använda värderingsfunktionen v(x) = x. (Om det inte gäller småpengar, exempelvis vid riktiga lotton med möjlighet till miljonvinster, då gäller dock inte denna regel och därmed kan det vara önskvärt att spela trots att du i genomsnitt förlorar varann krona du spelar.)

Ekonomiboken jag läste väljer att konvertera alla folks preferenser till pengar (dvs för mig är den rena luften över staden värd vad jag skulle vara beredd att betala för den), och definiera värdet av ett utfall för en person som summan av pengavärdet av allt den får. Målet är sedan att maximera totala värdet (vilket är delvis vettigt eftersom folk kan utbyta pengar fritt, mer om detta i ett senare inlägg). För samhället är det då bäst att alla individer maximerar sitt genomsnittliga värde, eftersom det när man summerar alla individers utfall ger det bästa totalvärdet med hög sannolikhet.

Som sagt väljer vi i SFM (Stochastic Financial Models) att använda ett utfallsrum bestående av pengavärden, och v är då den utilitetsfunktion vi ska maximera väntevärdet av. Jag har också nämnt att vi postulerar att v är konkav, så att man exempelvis hellre väljer 50000kr säkert än 100000kr med 50% sannolikhet. Detta medför alltså i viss mån en riskaversion (motvilja att ta risker). För att rationalisera lotterier måste vi dock låta v vara konvex, så att vi hellre väljer den potentiella vinsten på 1000000kr än den säkra besparingen på 10kr vi får av att avstå lottköpet.

If har kommit fram till att "i 15 av 16 olyckor där en gående avlidit är fordonets förare en man". (DN, Aftonbladet, Corren = Expressen)

Statistikern i mig reagerade direkt: Detta må vara av intresse för de fotgängare som föredrar att bli ihjälkörda av ena könet framför det andra, men det saknas kritisk information för att man ska kunna säga något om förarens påverkan på resultatet. Framför allt är det inte alls helt klart att "om alla körde som en kvinna skulle vi ha halverat antalet olyckor för flera år sedan".

Först och främst är frågan hur många män respektive kvinnor som hamnar i situationer där förarens körning utgör skillnaden mellan att en fotgängare dör eller inte. Man måste alltså väga in faktorer såsom:
* Hur stor andel av kvinnor/män har körkort?
* Finns det någon skillnad i hur ofta kvinnor/män kör bil, exempelvis av kulturella anledningar eller på grund av yrke?
* Finns det någon skillnad i hur ofta kvinnor/män kör tunga fordon, som har lättare för att mosa fotgängare?
* Tenderar ena könet att köra mer i riskområden än det andra (jämför exempelvis bostadsområden med motorväg)?

Först efter korrektion för dessa faktorer kan man komma med relevanta slutsatser, på formen "under identiska förhållanden har den genomsnittlige mannen X% större sannolikhet att köra ihjäl en fotgängare än den genomsnittliga kvinnan".

Antagligen kommer detta X vara positivt, och då är nästa steg att fråga hur stor del av effekten som beror på kausation jämfört med korrelation. Endast kausala effekter kan undvikas genom att omvandla alla förare till kvinnor.
* Manliga hantverkare verkar alltid prata i mobilen samtidigt som de kör bil. Gör de så för att de är män, eller för att de är hantverkare?
* Manliga taxichaufförer verkar alltid köra för fort. Gör de så för att de är män eller för att de är taxichaufförer?

När man tagit reda på detta kan man slutligen säga "under identiska förhållanden har den genomsnittlige mannen Y% större sannolikhet att köra ihjäl en fotgängare ÄN OM HAN VORE kvinna", vilket jag anser är den grund man ska använda för påståenden av formen "om alla körde som en kvinna...". (Egentligen behöver man också byta ordning på väntevärdesoperatorn med några andra aritmetiska operationer, men det är inte så noga.)

En fråga kvarstår dock: Är det önskvärt?

I artikelkommentarerna försvarar sig vissa män med att kvinnor ändå kör sämre, ur helhetssynpunkt. Det kanske är så att en säkrare körstil (rent hypotetiskt) kommer på bekostnad av effektivitet, i form av exempelvis längre transporttider, mindre kapacitet på vägarna, eller helt enkelt mindre nöje för förarna.

Då kan man fråga sig huruvida det är värt att rädda några fotgängares liv, i utbyte mot att transportkostnaderna i samhället ökar. Svaret på denna fråga är inte ett förbehållslöst ja - det faktum att samhället överhuvudtaget accepterar användandet av fordon innebär att vi tycker det är värt att döda några människor i utbyte mot effektivitet.

På svenska är det i huvudsak två djur som får nya namn när de blir till mat:
Nöt - ko
Fläsk - gris

På engelska har vi:
Beef - cow
Veal - calf
Pork - pig
Mutton - sheep
Venison - deer
(Calamari - shrimp)
(Scampi - prawn)

Spanskan har också några exempel, men det mest nämnvärda är förstås:
Pescado - pez

Idag höll Terence Tao en föreläsning för TMS om universalitet, vilket jag förstod som när ett system med många komplicerade mikroskopiska beteenden uppvisar enkla makroskopiska beteenden. Som exempel tog han universums atomer under gravitationslagen, vars makroskopiska beteende (bildandet av galaxer och kluster) vi förstår mycket väl trots att vi inte har en chans att följa varenda enskild atom. Ett annat exempel är kroppslängd, som följer en enkel normalfördelning trots (eller tack vare) att det finns en massa komplicerade faktorer som bidrar.

En intressant grej han tog upp är Benfords lag, som säger att begynnelsesiffran på tal i allmänhet är exempelvis en etta med 30% sannolikhet, men en nia endast i 5% av fallen. Som exempel har Wikipedia en graf över vilka begynnelsesiffror fysikaliska konstanter har:


En praktisk applikation för Benfords lag är att detektera påhittade eller manipulerade siffror, eftersom förfalskarna sällan ser till att de har rätt fördelning för begynnelsesiffrorna. På detta sätt har man kunnat avslöja såväl bokföringsbrott som valfusk.

Benfords lag gäller i allmänhet för storheter som utsätts för multiplikativa förändringar. Då är det rimligt att 1 är mycket vanligare 9 som begynnelsesiffra, eftersom den relativa skillnaden mellan 1... och 2... är 100%, medan skillnaden mellan 9... och 10... bara är 10%.

(För övrigt hörde jag nyligen ett webbradioprogram som diskuterade att barn ursprungligen räknar logaritsmiskt, så att skillnaden mellan 1 och 2 upplevs som större än skillnaden mellan 9 och 10. Om man ber dem sätta ut mitten mellan 1 och 9 anger de alltså 3 istället för 5. Detta försvinner sedan när barnet lär sig räkna 1, 2, 3, ...)

Föreläsaren drog sedan ett skämt, som gick ut på att Benfords lag även gäller för födelsedata. Som bevis frågade han publiken:
Vilka här har ett födelsedatum som börjar på 1? Ungefär 30%.
Vilka här har ett födelsedatum som börjar på 9? Ungefär 5%.
Vilka här har en födelsemånad som börjar på 9? Ungefär 5%.
Till sist brast det dock, när han frågade:
Vilka här har ett födelseår som börjar på 1?

För att ta reda på massan A hos ett svårvägt objekt kan man använda dig av differensvägning: Finn ett lättvägt objekt med massan B sådant att även kombinationen A+B är lätt att väga. Använd sedan lagen om konservation av massa för att få ut A = (A+B)-B. Exempelapplikationer:

Varor i förpackning: Professionella vågar (exempelvis i ICA MAXIs fiskdisk) brukar ha denna funktion inbyggd i form av en tareringsknapp. Man lägger på förpackningen först och tarerar (nollställer vågen). Sedan lägger man i varan och läser av resultatet.

Resväskor: Väg dig själv bärandes på väskan, och sedan bara dig själv. (Är detta trivialt att komma på om man aldrig hört det?)

Husdjur: Med Wii Fit plus kan man inte bara följa människors vikt utan även husdjurs. Husdjuret vägs då först i famnen på en människa, och sedan vägs människan ensam. Detta går förstås även att göra på vanlig våg.

Toalettavfall: Väg dig innan och efter toalettanvändning för att ta reda på vad ditt avföring/urin väger (varför du nu skulle vilja veta det, kanske FOR SCIENCE?). Om jag någonsin orkar ska jag prova att följa min vikt en längre period med vägningar innan och efter varje in- och uttag. Någon som vill låna ut en personvåg med noggrannare precision än 100g? Någon som har tips på kläder som är lätta att ta av och på sig över tio gånger om dagen?

För övrigt minns jag att jag för länge sedan läst om anorektiker som vägt allt som gick in och ut ur kroppen (inte genom differensvägning...), men missat att man även förlorar vikt genom exempelvis svett och döda hudceller. Det lättaste och tillförlitligaste sättet att hålla sin vikt torde vara att innan varje matintag ställa sig på vågen tillsammans med allt det man tänkt äta, och sedan lägga ifrån sig tills man kommer ner till den vikt man vill ha. Då väger man exakt det man vill efter måltiden. (Men sedan gäller det att svettas, gnugga bort döda hudceller, eller gå på toa för att kunna äta något nästa gång...)

Algebraic Topology: Föreläsaren är väldigt pure som vanligt. Han får pluspoäng för att han först introducerade två svåra problem (varav det ena var ifall rum av olika dimension kan ha samma topologi) för att motivera kursens existens. Det var också trevligt att jag kände igen lite idéer från Category Theory (fjärdeårskursen jag gick på i mitt första år utan att förstå något).

Integrable Systems: Första föreläsningen var repetition av Hamiltonianen från Classical Dynamics, samt introduktionen av ett integrabelt system som "i princip lösbara differentialekvationer".

Asymptotic Methods: Det dök upp så många studenter att vi var tvungna att byta till en större sal. Föreläsaren förklarade att han inte förstod ämnet, men att det skulle gå bra ändå. Vi har fått några exempel på vad asymptoter är.

Applications of Quantum Mechanics: Vi körde igång direkt med en ny idé, som (något förenklat) går ut på att om man vill uppskatta minimum för f så kan man gissa några x-värden, beräkna f(x) för dem, och använda det minsta av dessa som en övre gräns. Matematiskt: En övre gräns för minsta egenvärdet av en hermitesk matris A ges av (x,Ax)/(x,x) för vilket (nollskillt) x som helst. Fysikaliskt: En övre gräns för lägsta energinivån är energinivån hos vilken vågfunktion som helst. Föreläsaren delade ut föreläsningsanteckningar (som även finns på nätet), men sade att ifall vi börjar somna för att vi inte behöver anteckna själva så skulle vi kasta bort dem och låtsas som att vi inte fått några.

Waves: Vi har fått en massa exempel på var det går vågor, bland annat i marken, i kroppen, i rymden, i stjärnor och i trafiken. Vi ska dock bara behandla några stycken av dessa. Kursen kommer främst handla om metoder att lösa vågekvationerna, snarare än fysiken bakom dem.

Statistical Physics: Det mesta var välbekant för oss som gått Cosmology (som innehåller ett kapitel på Statistical Physics), men föreläsaren levde upp till förväntningarna. Kursen handlar om att ta Newtons ekvationer för de 10^23 partiklarna i en låda, och beskriva vad som kommer hända rent statistiskt. Föreläsaren sade att 2^(10^23) var ett "silly number", som han anser inte existerar på riktigt utan endast beskriver hur många teoretiska kombinationer det finns - man skulle aldrig kunna räkna upp dem.

Stochastic Financial Models: Föreläsaren började direkt med att deklarera att vi endast kommer behandla "von Neumann-Morgenstern"-preferenser, vilket innebär att alla utfall tilldelas ett utilitetsvärde och att ett val bedöms efter det genomsnittliga utilitetsresultatet. Det faktum att modellen förutspår att ingen någonsin köpper lotter nämndes också.

Further Complex Methods: Föreläsaren spenderade det mesta av tiden på att gå igenom kursplanen och förklara varför han gjort de ändringar han har gjort. I slutet gick han igenom något vi redan sett förra året, trots att han hade antytt att det var ett revolutionerande och annorlunda perspektiv.

Denna termin tar jag återigen officiellt 6 applied-kurser. Till skillnad från förra kommer jag dock (preliminärt) fylla de återstående två luckorna i schemat med en applicable- och en pure-kurs.

MWF 9: Waves (D)
MWF 10: Statistical Physics (D)
MWF 11: Stochastic Financial Models (D) istället för Numerical Analysis (D)
MWF 12: Further Complex Methods (C)
TuThS 9: Algebraic Topology (D) istället för Mathematical Biology (D)
TuTh 10: Integrable Systems (D)
TuTh 11: Asymptotic Methods (D)
TuThS 12: Applications of Quantum Mechanics (D)

De tre kurserna som låter mest intressanta (eftersom de är mest fysikaliska) är WAV (där vi äntligen kommer få veta varför svallvågor alltid har vinkel 2arcsin(1/3)), SP (som föreläses av den bästa föreläsaren i stan) och AQM.

Min DoS bekräftade mina misstankar att FCM och AM var extremt viktiga, men sade att IS bara var lite extra kuriosa. Angående NA berättade han att han i hela sitt liv bara utfört numeriska beräkningar en gång, och det var på en (programmerbar) miniräknare. MB hade han ingen koll på alls.

Att välja SFM över NA var inte svårt, trots att jag inte har några planer på att börja jobba på en bank. Däremot har jag velat lite mellan MB, AT, och eventuellt att ta CATAM-morgon (sovmorgon är uteslutet - att bryta sin dygnsrytm och vakna senare bara för att man kan är absurt).

MB börjar med lite vardagliga saker såsom populationstillväxt, men avslutas med "Neural computation: Hodgkin-Huxley model of action-potential propagation, unsupervised and supervised learning." vilket låter coolt. Jag är dock (oresonligt) skeptisk till hela konceptet att detaljstudera något som inte är hårda naturlagar utan har uppstått genom en slumpbaserad process över miljardtals år - om vi en dag stöter på utomjordiskt liv kommer det ju antagligen inte att fungera likadant som vårt!

AT å andra sidan verkar vara en väldigt ren pure-kurs, vilket jag har saknat ibland. Den har dessutom väldigt låga förkunskapskrav, så jag har en god chans att hänga med iallafall i början. När jag sedan ger upp kan jag byta till MB.

Enligt Aftonbladet har spansk domstol bestämt att Ryanair inte får ta ut sin avgift på 40 euro för att skriva ut boardingkort åt glömska passagerare.

Personligen ser jag avgiften som ekonomiskt incitament precis som alla andra avgifter Ryanair har: De har identifierat vad som kostar pengar och tar ut hutlösa avgifter på det för att uppmuntra resenären att göra det själv. Jag tror exempelvis på att bagageavgiften gör att folk tänker efter en extra gång innan de tar med sig onödiga saker på semesterresan, och att de försöker att få med sig väskan ombord istället för att belasta bagagehanterarna med den. Detta är mer effektivt och sparar därmed pengar för alla.

I det aktuella fallet är det i och för sig antagligen inte så stor skillnad om passagerare skriver ut boardingkortet själv eller bekostar att någon på flygplatsen gör det åt dem, men många bäckar små...

Enligt Aftonbladet säger internationell lag att flygbolaget måste skriva ut boardingkort till sina passagerare. Ifall det inte står i lagen att flygbolagen måste använda sig av boardingkort skulle man dock kunna kringgå lagen genom att slopa konceptet "boardingkort" helt och hållet och införa en "boardinglapp" som är exakt samma sak men inte lyder under lagen.

Det verkar som att Ryanairs terms and conditions som man måste godkänna vid biljettköp innefattar en klausul om denna avgift. Då är frågan huruvida rättigheten till gratis boardingkortutskrift på flygplatsen är tvingande, så att passagerarna inte kan avtala bort den.

I slutet av Air & Business Travel News artikel hotar Ryanair med att sluta skriva ut boardingpass överhuvudtaget på spanska flygplatser. Det vore absurt om lagen är formulerad så att flygbolag inte får ta ut avgift för utskrift, men däremot får vägra utskriften helt.

Idag åt jag min första salladslunch för terminen, dvs jag åt sallad istället för huvudrätt. Som sagt tar man sallad numera i skålar istället för halvmånformade tallrikar. Huruvida det blir mer elller mindre mängd har vi inte lyckats komma fram till. Dock heter det fortfarande "Salad Crescent" i systemet, och de har höjt priset från 76p till 80p.

På tal om månens form: Månens form kommer av att den är en sfär som är upplyst från ett håll av solen. Månskärans yttre kant är alltså alltid en halvcirkel som går från pol till pol, medan den inre kanten är en halvellips från pol till pol.


De flesta tecknade avbildningarna av månen ser dock inte ut så. Det vanligaste felet jag noterar är att ytterkanten är längre en en halvcirkel och/eller att innerkanten också är en cirkel. Fallet då innerkanten har ungefär tre gånger så stor radie som ytterkanten kan uppstå vid månförmörkelse, men övriga fall kan man bara få till genom att hålla upp exempelvis en tallrik framför fullmånen.

En gång för länge sedan höll någon en föreläsning för TMS (Trinity Mathematical Society) om epistemisk osäkerhet. Här är mina funderingar kring det vederbörande sade. Sammanfattning i fetstil.

Epistemisk osäkerhet

En illustration föreläsaren använde för vad epistemisk osäkerhet är är följande:
Han tar upp en slant och säger att han ska singla den. "Vad är sannolikheten för krona?"
Han singlar slanten och täcker för den med handen. "Nu då?"
Han lyfter lite på handen och kikar på resultatet utan att visa publiken. "Nu då?"

Svaret på alla frågor är "50%", men det är bara första gången denna sannolikhet mäter äkta slump (om vi antar att slantsingling är helt slumpmässig). Andra gången är resultatet redan bestämt, och "50%" mäter bara osäkerheten kring resultatet. Sista gången är "50%" bara publikens uppskattning - för föreläsaren är det "100%" eller "0%".

Epistemisk osäkerhet är osäkerhet om ett redan bestämt utfall som uppstår hos en observatör på grund av avsaknad av information. När du går till läkaren så är du antingen sjuk eller inte, men läkarens undersökning är behäftad med epistemisk osäkerhet.

Jag minns inte vad hans poäng med att ta upp detta var, men det jag tycker nu är att epistemisk osäkerhet och slumposäkerhet bör behandlas lika. Därmed faller min tidigare idé att "det är ingen idé att oroa dig för slutbetygen du ska få imorgon för de är redan satta". Dock gäller fortfarande "det är ingen idé att oroa dig för slutbetygen du ska få imorgon för du kan inte påverka dem och oron är inte produktiv". (Detta gäller bara de som inte tror att det finns högre makter som kan påverkas av ens oro och förändra saker som redan hänt.)

Att värdera osäkerhetsuppskattningar

Nu menar jag med "osäkerhet" både äkta och epistemisk sådan. Ett exempel på när någon uppskattar osäkerhet är vid väderförutsägelser. Då kan man höra saker såsom "Det är 75% chans att det regnar imorgon". Men hur kollar man om det verkligen är 75%? Vi har bara en chans att testa påståendet - vänta tills imorgon och se - och då blir resultatet antingen "Det regnade" (100%) eller "Det regnade inte" (0%). Det vi måste göra är att samla in en mängd förutsägelser och resultat, och använda någon metod för att mäta hur bra förutsägelserna stämmer överens med verkligheten.

En naiv metod är följande: Samla ihop alla dagar då meteorologen förutspådde 75% chans till regn, och kolla om det verkligen regnade i 75% av fallen. Detta missar dock en väldigt viktig sak vi önskar från förutsägelser: Specificitet. Vem som helst kan slå upp att det regnar 278 dagar om året på Hawaii, och förutspå 75% regnchans varje dag. Detta är förstås mycket mindre användbart än någon som säger 0% och 100% men missar lite då och då.

En mer sofistikerad metod är att använda ett poängsystem: Den som gissar rätt vinner poäng och den som gissar fel förlorar, men ju säkrare man är desto fler poäng står på spel. Därmed bör den som ger väldigt specifika förutsägelser tjäna fler poäng än den som ger samma medelmåttiga förutsägelse varje gång.

Nu kan man återigen vara naiv och tilldela (X-50) poäng till den som angett X% sannolikhet för den korrekta resultatet, men då uppstår ett annat problem: Låt säga att du har förutspått att det kommer regna med 75% sannolikhet. Då kommer du vinna 25 poäng i 75% av fallen och förlora 25 poäng i övriga 25%. I genomsnitt får du 25*50% = 12.5 poäng per gång. Om du istället ljuger och påstår 100% säkerhet, då får du istället 50*50% = 25 poäng per gång. Detta system uppmanar alltså meteorologen att ljuga och alltid ange 0% eller 100% för regn. Mer användbart än det förra, eftersom du har en indikation på vilket som är mest sannolikt, men inte optimalt.

Istället för detta linjära system bör man till exempel använda ett kvadratiskt system. I ett exempel vi fick göra under föreläsningen skulle vi fördela 10 poäng mellan två motsatta påståenden, där 10+0 betyder att man är bombsäker på det första medan 0+10 betyder att man är bombsäker på det andra. Formeln som användes för poängutdelning var (25 - X^2), där X är poängen man satt på det felaktiga påståendet. Är man bombsäker och har rätt får man alltså 25 poäng, men om man är bombsäker och har fel får man -75.

Det går att visa att detta poängsystem gör att man i längden tjänar mest på att påstå den sannolikhet man själv tror på. Tag återigen som exempel att du tror på att det regnar 75% av tiden på Hawaii. Om du också säger detta, får du +18.75 poäng i 75% av fallen och -31.25 poäng i resten, vilket totalt ger 6.25 poäng i genomsnitt. Hade du istället påstått 100% hade du fått +25*0.75-75*0.25 = 0 poäng i genomsnitt. (Den som vet exakt vilka dagar det kommer regna får 25 poäng varje gång.)

Det är lätt att se med blotta ögat att det kvadratiska systemet avskräcker folk från att överskatta sin säkerhet: Om du anger 10 istället för 9 så får du en extra poäng när du har rätt, men 19 extra minuspoäng när du har fel.

Vi har nu ett system som givet en mängd förutsägelser och resultat kan ge ett siffervärde på hur bra förutsägelserna var. Detta värde i sig säger förstås inget, men det kan användas för att jämföra flera olika förutsägelsemetoder: Är SMHI, yr.no, farfars spåkula eller mormors gikt bäst på att förutspå regn?

Notera att systemet inte tar någon hänsyn överhuvudtaget till vilka metoder som används för att göra dessa förutsägelser. Den som tycker att systemet har fångat essensen av vad vi menar med en bra förutsägelse (försöker ange så korrekt procentsats som möjligt, och ju längre bort från 50% desto bättre) tycker förstås att det är positivt att systemet struntar i irrelevanta saker. Den som endast accepterar vedertagen vetenskap, även om spåkulan ger bättre resultat enligt detta system, måste tycka att systemet har missat något viktigt i definitionen av vad en bra förutsägelse är.

Innehållet mest störst intressanthet/förståelighet-kvot är fetstilat. Missa inte biten längst ner!

Newtons lagar

Det är Newtons andra lag som säger att accelerationen a för en partikel som påverkas av en total kraft F är given av formeln F = ma, där m är partikelns massa. Newtons första lag är bara specialfallet F = 0.

Newtons tredje lag säger att varje kraft har en motkraft, dvs om en partikel A påverkas av en kraft, så kommer denna kraft från någon annan partikel B, och B påverkas av samma kraft fast åt andra hållet. De flesta krafter kan man alltså tänka sig som spända eller hoptryckta fjädrar mellan par av partiklar.

Potentialer

Potentialer i en dimension är jättelätta att förstå och analysera: Tänk dig en funktionskurva och en boll som kan rulla fram och tillbaka på den under inverkan av gravitationen. That's it! (Bortsett från den lilla detaljen att vi ignorerar hastigheten i vertikalled.) För enkelhet låter vi bollens massa m = 1.

Tag som en exempel den enklaste potentialen, harmoniska oscillatorn V(x) = x²:

Oavsett hur man sätter en boll i rörelse i denna kommer den oscillera fram och tillbaka i en ren och fin sinusrörelse (under förutsättning att vi ignorerar vertikala hastigheten).

En liten mer avancerad potential är följande:

En boll som kommer inrullande från vänster och har för låg energi (hastighet) kommer rulla upp en bit på kullen, vända och rulla tillbaka igen med samma hastighet (reflektion). Om den har tillräcklig fart kommer den över hindret och fortsätter på andra sidan (transmission), fast med lägre hastighet. På samma sätt kan en boll från höger reflekteras eller transmitteras (fast med högre sluthastighet). Dessutom kan bollen oscillera i gropen utan tillräcklig energi att ta sig upp (bundet tillstånd).

Ett intressant specialfall ovan är att bollen kan ligga i gropen med tillräcklig energi att den kommer upp ovanför vänstra grundnivån, men inte tillräckligt för att kunna ta sig ut till vänster genom att rulla över kullen. I klassisk mekanik kommer bollen då stanna i gropen, men i kvantmekanik har bollen en viss sannolikhet att dyka upp på andra sidan kullen. Detta fenomen kallas kvant-tunnling, och kan användas för att modellera exempelvis radioaktivt sönderfall: Den partikel som utsänds vid alfasönderfall modelleras som fastlåst i en potentialbrunn i kärnan, men med tillräckligt mycket energi för att existera en bit bort. Varje tidsenhet har den då en viss sannolikhet att tunnla sig ut och lämna kärnan.

Så till själva matten.
Vi börjar med bevarande av total energi (kinetisk+potentiell): x'(t)²/2 + V(x(t)) = E.
Derivera med avseende på tid (använd kedjeregeln): 2·x'(t)·x''(t)/2 + V'(x(t))·x'(t) = 0
Dividera bort x'(t) (ignorera fallet x'(t) = 0): x''(t) + V'(x(t)) = 0
Flytta över: x''(t) = -V'(x(t))
Newtons lag F = a: F = -V'(x(t))

Läser man uppifrån och ner ser vi ett bevis att kraften F(x) är -V'(x). Läser man nerifrån och upp ser man att om kraften F(x) bara beror på positionen, så bevaras totala energin. (Nerifrån och upp ser vi också ett sätt att påbörja en lösning av differentialekvationer på formen x'' = F(x).)

I flera dimensioner är inte varje kraft F(x) (negativa) derivatan av en potential V(x). De krafter som är det kallas konservativa krafter, eftersom de konserverar totala energin. Funktionen F(x) kallas även för ett potentialfält i detta fall.

Exempel: Satellitbanor

Gravitationskraften från en planet i tre dimensioner har potential V(x) = -GM/|x|. Det är dock inte så lämpligt att ta ett endimensionellt tvärsnitt av detta för att analysera problemet, eftersom man då bara kan fundera på de banor som går rakt in eller rakt ut från planeten - detta är inga omloppsbanor!

Däremot räcker det att studera problemet i två dimensioner, eftersom alla omloppsbanor ligger i ett enda plan. I detta plan är det lämpligt att använda polära koordinater: r(t) är avståndet till planeten, och φ(t) är vinkeln.

Rotationshastigheten φ'(t) är starkt kopplad till avståndet genom bevarande av rörelsemängdsmoment: h = r²φ'(t) är konstant. Rörelseenergin är (r'² + r²φ'²)/2 = r'²/2 + h²/2r², så den totala energin är: r'²/2 + h²/2r² - GM/r = konstant.

Vi tolkar denna ekvation som r'²/2 + V(r) = konstant, där V(r) = h²/2r² - GM/r kallas effektiva potentialen (det fungerar som en potential, men är inte det ur fysikaliskt perspektiv).

Vi ser att skillnaden mot den ursprungliga gravitationspotentialen är termen h²/2r², som kommer från den tangentiella hastigheten i uttrycket för rörelseenergi. Detta säger helt enkelt att när vi bara tittar i r-led så glömmer vi att satelliten även rör sig i sidled, och därmed har vi missat en bit av rörelseenergin.

Den generiska bilden av den effektiva potentialen är:

Vi ser att hur man än startar sin satellit (med den givna rörelsemängdsmomentet) så kommer den aldrig falla in till centrum av planeten som befinner sig i vänsterkant. Däremot kommer satelliten i vissa fall ha tillräckligt med energi att ta sig ut till oändligheten i högerkant. De vanliga omloppsbanorna är då satelliten oscillerar fram och tillbaka i gropen.

Exempel: Satellitbanor runt svarta hål

Runt svarta hål är gravitationen så stark att formeln V(x) = -GM/|x| inte gäller. Istället får vi (med lämpliga enheter) den effektiva potentialen V(r) = (1 - 1/r)(1 + h²/r²)/2. Den stora skillnaden här är att potentialen inte blir oändlig när r går mot noll, utan den blir negativt oändlig. Därmed kan partiklar falla in till hålets mitt, till skillnad från i Newtonsk mekanik. Det finns två generiska fall:



Om rörelsemängdsmomentet h inte är stort nog sluttar potentialen alltid in mot centrum. Alla banor med så lite fart runt måste alltså antingen falla in till hålets mitt, eller flyga ut till oändligheten.

Om rörelsemängdsmomentet är stort nog har potentialen en puckel. Förutom föregående fall finns det också riktiga omloppsbanor, där satelliten ligger nere i gropen och oscillerar.

För den som vill leka med detta finns en java-applet här: http://www.fourmilab.ch/gravitation/orbits/

Hur kommer det sig att ordet "äpple" och dess översättningar dyker upp i namn för olika saker, där "frukt" hade passat bättre eftersom det inte finns någon slående likhet med äpplen?

* Granatäpple / Pomegranate / pomme-grenade - kärnigt äpple
* Apelsin / Apfelsine - kinaäpple
* Pomme de terre [potatis] - jordäpple (jfr "pommes frites")
* Pomme de pin [kotte] - talläpple
* Pineapple [ananas] - talläpple (kommer från namnet för kotte)
* Cashewäpple / Pomme de cajou - cashewäpple (Tydligen är cashewnöten ett frö som växer i änden på en paprikalliknande frukt.)
* Stjärnäpple / Star apple [cainito] - stjärnäpple (inte samma sak som carambola - stjärnfrukt)
* Pomme du lait [cainito] - mjölkäpple
* Adamsäpple / Adam's apple / Pomme d'Adam - Adams äpple (enligt Wikipedia är det bara påhitt att den förbjudna frukten skulle vara ett äpple, men där anges en pun som orsaken: "malus" på latin betyder både "ond" och "äpple".)

För ett tag sedan byggdes Sainsbury's om, och i samband med detta tog de bort mina älskade syltmunkar från sortimentet. Nu är syltmunkarna tillbaks, till priset 20p/st eller 40p för tre (dvs 13p/st). Det finns också ett fempack för 60p (dvs 12p/st). I fempack säljs även vanlijmunkar, för 69p (dvs 14p/st).

När jag kom till kassaautomaten kostade munkarna dock 25p för en eller 50p för tre (dvs 17p/st). Jag kommer alltså definitivt köpa fempack i framtiden.

Idag när jag läste min College Bill såg jag för första gången att Trinity College är en "Registered Charity" (nummer 1137604). Faktum är att minst 29 av universitetets 30 college är välgörenhetsorganisationer - den enda jag inte lyckats finna är Darwin College. (Någon som vet varför? Är det av skatteskäl?)

Tidigare hette välgörenhetsorganisationen "Trinity College Within The Town And University Of Cambridge Of King Henry The Eighth's Foundation" (Urskillningslös versalisering uppnådd genom Shift+F3 i Word eftersom originalet är i ALL CAPS), vilket antagligen är collegets officiella namn.

Här är de 9 aktuella collegevälgörenhetsorganisationsnamn som inte är trivialt uppbyggda av collegens trivialnamn tillsammans med ett urval ur "The Master/Keeper/President and Fellows and Scholars of ... in the University of Cambridge", i avtagande längdordning:

* Gonville and Caius College: Gonville And Caius College In The University Of Cambridge Founded In Honour Of The Annunciation Of The Blessed Mary The Virgin
Christ's College: Christ's College Cambridge In The University Of Cambridge First Founded By King Henry Vi Of England And After His Death
* Pembroke College: The College Or Hall Of Valence Mary Commonly Pembroke College In The University Of Cambridge
* Corpus Christi College: College Of Corpus Christi And Of The Blessed Virgin Mary In The University Of Cambridge
* Queens' College: The Queens' College Of Saint Margaret And Saint Bernard In The University Of Cambridge
* St Catharine's College: The College Or Hall Of Saint Catharine The Virgin In The University Of Cambridge
* Sidney Sussex College: The College Of The Lady Frances Sidney Sussex In The University Of Cambridge
* Magdalene College: The College Of St Mary Magdalene In The University Of Cambridge
* King's College: The King's College Of Our Lady And Saint Nicholas In Cambridge

Denna söndag, och även nästa, står det "Sunday Brunch" på lunchmenyn. Det innebär att vi erbjuds det som brukar vara frukost (såsom bacon, bönor, friterat bröd och svamp), fast till lunch. Fast det finns även efterrätt.

Jag noterade också att serveringen kommer vara öppen hela förmiddagen i framtiden, så man kan köpa något litet att äta även mellan frukost- och lunchtid (som även dessa är förlängda jämfört med tidigare).

Innan jag lämnade Linköping såg jag en reklam som sade att standbyläget på hemelektroniken slösar el utan att tillföra något. Jag håller inte med - standbyläget på TV-apparaten innebär att man kan slå på och stänga av TV:n med fjärrkontrollen istället för att gå fram till den.

Det kanske inte låter som en så viktig grej att slösa el på, men å andra sidan är det inte så mycket el som slösas heller. Vår nya TV i köket drar 750 gånger så mycket ström när den är på som när den är i Standby. Man slösar därmed ungefär lika mycket ström på att ha den i standby i ett dygn, som att ha den igång i onödan under två minuter (exempelvis medan man går på toa, eller under reklampauserna som brukar vara längre än så).

Något relaterat är frågan om Sleep/Viloläge eller Hibernate/Vila på datorn. Både sleep och hibernate bryter huvudströmmen precis som när man stänger av datorn helt, med skillnaden att RAM-minnet bevaras så att programmen man har igång fortsätter köra när man sätter på datorn igen. Vid Sleep hålls RAM-minnet igång med lite ström, medan hibernate innebär innehållet sparas ner på hårddisken innan all ström bryts.

Jag vet, sedan tiden då mitt batteri fungerade, att min dator drar 60 gånger så mycket ström i gång som den gör i sleep (1% per minut jämfört med 1% per timma).

Idag uppmätte jag nedstängnings- och uppstartstid för olika alternativ, där uppstartstiden definieras som tiden från att startkommando ges tills processoranvändningen går ner till försumbar nivå:
Sleep: 11s + 16s = 27s
Hibernate med en massa program igång: 69s + 111s = 180s
Hibernate utan en massa program igång: 34s + 72s = 106s
Full omstart: 53s + 245s = 298s

Den första slutsatsen är att full omstart tar mest tid och därmed även mest energi. Man ska alltså endast göra det när det finns goda skäl, såsom installation eller allmän skräprensning.

Den andra slutsatsen är att om man vill ha sina program igång så är det energimässigt mer fördelaktigt att sleepa datorn vid avbrott mindre än 2.5 timme, medan man ska ta hibernate om avbrottet är längre.

Själv kör jag alltid sleep, för att slippa vänta de knappa två minuterna på att datorn ska komma ur hibernation. Undantaget är över natten när jag är i England, då jag kan låta datorn starta upp automatiskt ur hibernation och väcka mig. Det gäller bara att jag också kommer upp ur sängen och fram till datorn inom 10 minuter - annars har den slösat bort de 10 timmarnas sleepström jag försökte spara!

Efter ett och ett halvt års ombyggnad är äntligen nya köket och serveringen klara. Det nya köket sägs vara toppmodernt med bland annat induktionsspisar, men det märker vi inte av. Det som märks är att vi numera inte tar vår mat i Hall, utan i ett eget serveringsområde på andra sidan korridoren.

Det är positivt att de har ställt de tre huvudrätterna (Main Course, Vegetarian Main Course och Chef's choice) på separata ställen med separata köer, men en sak som har blivit sämre är att övriga saker finns utspridda över hela rummet utan en tydlig linjär ordning, så att folk kommer springa kors och tvärs i jakt på det de vill ha. Då föredrar jag St. John's layout, där allting ligger längs en enda U-krök så att alla går åt samma håll (med möjligheter för den som vill hoppa över saker att göra så). Två neutrala förändringar är att salladen numera tas i skålar istället för halvmånformade tallrikar, samt att man får ta efterrätten själv.

I Hall har vi alltså fått mer plats att sitta och äta nu när serveringen flyttat ut, vilket kommer innebära att alla förstaårselever kommer få plats under matriculation dinner. Till vardags är enda skillnaden att borden står i fyra rader om fem, istället för fem rader om fyra. Detta innebär att de obekväma (för höga) väggbänkarna inte längre används, utan alla bord kantas av stolar eller träbänkar i lagom höjd. Det innebär också att likheterna med Hogwarts ökar.

En till förändring är att öppettiderna förlängts. Framförallt öppnar Hall numera 45 minuter tidigare både till lunch och middag, vilket är så tidigt att det antagligen inte kommer att vara någon köbildning innan öppning. Tidigare har middagskön kunnat bli upp till 20 minuter lång vid öppningsdags.

Innan landningen flög vi igenom några moln och det var tidvis stark turbulens. Då observerade jag ett intressant fenomen: Med solen i ryggen tittade jag ut genom fönstret, och såg en pytteliten cirkulär regnbåge, mycket mindre än de två regnbågar jag hört talas om tidigare. Det är svårt att uppskatta cirkelns storlek, men dess diameter var ungefär halva längden på flygplansskuggan mot molnen, och skuggan var ganska nära - så nära att den kändes stor, men så långt bort att jag kunde se hela skuggan genom fönstret.

Jag visste inte när vi skulle landa egentligen, men jag visste att vi var försenade eftersom det inte blev någon fanfar vid landningen. Egentligen skulle vi ha landat 13.30, vilket skulle ge mig 55 minuters väntetid till tåget eller 90 minuter till bussen. Nu hann jag med tåget iallafall, och fortfarande med god marginal.

Marginalen var så god, att jag spenderade lite tid på att försöka hitta en snabbare väg till tåget. Jag har konstaterat sedan tidigare att ankomsthallen ligger i ena änden av den drygt 300 meter långa terminalbyggnaden som ligger rakt ovanför spår 1 och 3, medan Cambridge-tåget avgår från spår 2 i andra änden bortom byggnadens slut.

Denna gången konstaterade jag att den enda färdvägen som inte innebär 100 meter omväg på grund av en lång svagt sluttande asfaltsramp i två delar är nerför rulltrapporna i mitten av byggnaden. Två rulltrappor förbinder byggnadens plan med markplan där bussarna står, och ytterligare två rulltrappor förbinder markplan med källarplan där tågen går. Dock är det bara de två nedre rulltrapporna som går åt varsitt håll, de två övre rulltrapporna går båda uppåt...

För övrigt går tågresan till såhär: Jag köper min biljett Stansted-Cambridge i en automat på tågstationen. Det är en "Anytime Day Single", vilket innebär att jag får åka med vilket tåg som helst, vilken rutt som helst, vilket tid som helst, samma dag som jag köper biljetten. (Huruvida konduktören skulle acceptera denna biljett ombord på ett tåg i en helt annan del av landet återstår att se.) Ombord på tåget får jag välja plats fritt, men i vissa stolar sitter det lappar där det står vilka sträckor platserna är bokade, vilket jag antar har skett via internet. (Böter för otillåten användning av platsen är £50, medan otillåtet avlägsnande av lappen kostar £200.) Konduktören ombord klipper min biljett, men det går också bra att köpa biljetten av denne, fast då kan man riskera att gå miste om rabatterbjudanden i de fall man har stigit på vid en station där biljettluckan var öppen. Efter avstigninen i Cambridge (som är den andra stationen på vägen) måste jag stoppa biljetten i spärren för att komma ut från stationsområdet.

På tåget såg jag en kille som bar shorts, trots det kalla vädret (även om det var varmt för mig som kommit från Sveriges minusgrader). Det berodde antagligen på att hans kropp var av metall från strax ovanför knäna och neråt. Frågan är om han hade shortsen bara för att han inte hade något behov av att hålla metalldelarna varma, eller om långbyxor hade hämmat metallbenens funktion.

När vi rullade in på stationen i Cambridge noterade jag att den guidade buswayen förökat sig från en betongbana till två, vilket var en klen tröst i sammanhanget då projektet med kantstyrda bussar från Cambridge till grannstäderna nu är över 1.5 år försenat.

En annan sak jag noterade var skylten som välkomnar tågresenärerna till "Cambridge - Home of Anglia Ruskin University". Jag antar att det är med glimten i ögat som ARU marknadsför sig som ett ANNAT universitet i staden som är världskänd för universitetet med samma namn.

Mitt flyg skulle avgå från Skavsta 12.15, men på grund av väglaget vågade jag inte ta flygbussen som anländer 11.15 (vilket skulle ge mig 20 minuters marginal tills incheckningen stänger). Därmed fick jag gå upp tidigt på morgonen för att ta 7.15-bussen med ankomst 8.45.

Denna gång var den första som jag förköpte min flygbussbiljett på nätet. Normalt ungdomspris Enkel/ToR är 130kr/199kr medan E-biljetten kostar 99kr/198kr, så jag köpte en enkel E-biljett. Det gick att få biljetten som SMS för 3kr extra, vilket jag valde, men det verkar som att det ändå bara kostade 99kr. När jag fick se SMS-biljettens 36-siffriga kontrollkod valde jag dock att skriva ut E-biljetten som hade (2D-)streckkod istället. (För övrigt gäller biljetten i valfri riktning under tre månader, så om jag av någon anledning inte lyckades komma med flygbussen så skulle jag kunna använda biljetten på hemvägen eller låta Matilda använda den när hon besöker mig.)

Jag somnade strax efter att vi kommit ut på motorvägen vid Tallboda. Under resan vaknade jag i rondellen vid Max i Norrköping (och hade därmed missat stoppet i Norrköping, trots att jag brukar vakna när det står still), vid avfarten i Nyköping, vid sista rondellen, och slutligen när vi rullade in på Skavsta. Min mobil visade exakt 8.45 då, så antagligen hade jag hunnit även med den senare bussen.

Jag spenderade den första biten av väntan på Skavsta med att läsa anteckningar från tredjeårskursen Logic and Set Theory som jag gått och lyssnat på i mitt första år. Det kanske blir ett litet blogginlägg om de intressanta delarna därifrån senare.

Sedan åt jag lunch, hamburgare med pommes för 120:-, på den enda restaurangen. Köttet var inte så intressant, men det som inte var själva burgaren i burgaren var gott, och pommesen var utsökt.

Idag vägde de allt handbagage innan säkerhetskontrollen, så den som brukar använda det gamla tricket att stoppa allt tungt i handbagaget för att slippa betala överviktsavgifter får flytta upp till nästa nivå som är att ta på sig flera lager kläder.

Vid säkerhetskontrollen blev de tre säkerhetskontrollanterna lite konfunderade över innehållet i min väska. De backade tillbaks den i röntgenmaskinen en gång, och sedan körde de ut den och stoppade in den igen för att få en bild från en annan vinkel. Till slut blev de nöjda och jag fick min väska. Jag frågade dem om det var min gurka (halv, inlindad i plastfolie, bra vätskekälla) som hade orsakat bryderiet, och de svarade jakande.

Vid gaten hade de tagit bort de stolar som det var tveksamt ifall de tillhörde kön eller inte, dit folk kunde tränga sig för att få en sittplats för att sedan ställa sig upp mitt i kön när det var boardingdags. Istället hade de byggt en sicksackbana där folk fick stå och köa. Banan gick fram och tillbaka sex gånger, och jag som var en av de första på plats kände mig lite som en fadderist när jag gick där i räta vinklar fram och tillbaka. Många andra passagerare valde att klämma sig förbi längs med väggen istället.

Ombordstigningen flöt på utan problem, och jag satte mig på bakersta raden som vanligt. Någon minut efter att vi lyft somnade jag.

Idag hällde jag ut fyra burkar utgången öl i vasken. Det var så högt tryck i dem att det sprutade ut skum även när jag öppnade burkarna uppochner. Huruvida detta är normalt vid rumstemperatur eller berodde på utgångenheten vet jag inte, eftersom jag inte har någon kontrollölburköppning att jämföra med.

För övrigt ser ölskum ut som halvvispad äggvita.

Och öl är äckligt eftersom det smakar som kolsyrat vatten med ölsmak (duh?).

Här är en god approximation till vad saker kostar på McDonald's, baserat på kvitto- och minnesfragment. Rätta mig gärna där jag har fel. Notera dock att olika restauranger kan ha olika priser och att priserna varierar över tid.

Liten, mellan, stor dricka/pommes kostar 13:-, 16:-, 19:-.

Standardmenyer (burgare + mellandricka + mellanpommes) kostar 18:- mer än bara burgaren, medan plusmenyer (burgare + stordricka + storpommes) kostar 23:- mer än bara burgaren. Därmed sparar man 14:- respektive 15:- på att köpa meny.

Detta slås in i kassan genom att burgarna och läsken slås in som vanligt, medan pommesen slås som "Mellan PF (meny)" för 2:- eller "Stor PF (meny)" för 4:-.

Ett undantag från detta system är att Cheeseburgare (och förmodligen Hamburgare) kostar 10:- normalt, men 23:- när de kombineras i menyn (t.ex. "Cheese (Lilla Menyn)"). Besparingarna för att köpa meny blir då bara 1:- respektive 2:-.

Exempel på andra burgarpriser: QP Cheese 43:-, McFeast 44:-, Big Mac 49:-.

För några dagar sedan ringde jag Flygbussarna och frågade ifall dem sista avgången från Skavsta till Linköping skulle vänta in ett försenat plan från Gatwick. Jag fick till svar att den skulle det (vilket också bekräftas av texten i högerspalten i deras pdf-ficktidtabell online, som jag inte länkar till eftersom den bara är giltig fram till mars) - bussen står kvar till 30 minuter efter att sista planet landat.

Dock väntade inte bussen, utan den avgick 01.00 efter att väntat en timme, precis efter att passagerarna från Gatwick-planet kommit till passkontrollen. Dock fixade Flygbussarna en taxi istället för de tre passagerare som skulle till Östergötland. Jag hoppas att detta förfarande är standard.

Igår kväll fick jag delvis svar på en fråga jag aldrig funderat på: Hur tillverkar man hushållspapper?

Jag hade kommit ner till sista papperet på rullen - det som är knögligt och klibbar fast mot kartongen - och när jag tagit loss det och sträckt ut det såg jag att dess kanter (uppe och nere) var ojämna, dvs hackiga. När jag knöglade till det igen längs vecken som kom från att det hade suttit på rullen blev kanten dock åter jämn och fin.

Slutsatsen är att hushållspappersrullarna tillverkas genom att ett brett papper rullas upp på en bred rulle, och sedan klipps till till lagom stora bitar. Om jag funderat över denna fråga tidigare skulle jag antagligen ha kommit fram till att detta var den mest rimliga lösningen, men nu fick jag den spoilad utan ha fått fundera på det.

Edit: Plastfolie tillverkas dock antagligen inte såhär, eftersom folien är lite smalare än rullen.

Tydligen håller Sverige på att få en 200-kronorssedel. Då saknas bara ett återinförande av 2-kronan innan svenska kontantsystemet är konsekvent igen (dvs 1 2 5 10 20 50 100 200 500 1000). Själv använder jag dock nästan alltid kort.

Förra terminen (två månader) använde jag kontanter endast ett fåtal gånger: Jag reglerade en skuld med Lukas och en med Ian (vilka jag hade handlat på Sainsbury's med mitt kort för) och köpte två tvättkort i p(orters' )lodgen.

Under detta jullov (en månad) var det ungefär likadant: Jag har fått lite kontanter av folk som jag lagt ut pengar för (med kortet). Den enda gång jag använt kontanter fast jag kunde ha använt kort var på pizzerian för några dagar sedan.

Följande är vad jag har listat ut om att posta brev.

Det finns två alternativ: 1:a-klass (utdelning vardagen efter) och ekonomi (utdelning inom tre vardagar). 1:a-klass är default, och man måste skriva "B" på kuvertet för att det ska bli ekonomi.

Grundprisenheten för de två alternativen är 6:- respektive 5:50. Priset för brev upp till 20, 100, 250, 500, 1000 respektive 2000 gram är 1, 2, 4, 6, 8 respektive 12 grundprisenheter.

Det finns frimärken med valörer (exempelvis 6kr), men det finns också valörlösa frimärken - en typ för 1:a-klassbrev och en annan för ekonomibrev - vars värde motsvarar grundprisenheterna. (Om jag förstått systemet rätt är det alltså lönsamt att köpa valörlösa frimärken, eftersom valörfrimärken tappar värde när priserna stiger.)

Julfrimärken kostar lika mycket som ekonomibrevsfrimärken och kan även användas som sådana efter jul. Dock förbehåller posten sig rätten att dra ut på utdelningen av dessa (mer än tre vardagar) innan jul, på grund av den stora mängden julkort. Frågan är om detta även gäller ekonomibrevsfrimärken, eller om man skulle kunna "spara" lite tid (på bekostnad av julstämning) genom att frankera sina julkort med ekonomibrevsfrimärken istället. Denna jul tog mina julkort en vecka på sig att komma fram, så ifall jag kommer ihåg nästa år kommer jag att skicka 1:a-klass, trots de extra 50 örena.

Utrikesbrev kan endast skickas som 1:a-klass, och måste märkas med blå prioritaire-etikett (troligen eftersom 1:a-klass inte är default utomlands). För brev under 20 gram är priset det dubbla jämfört med inrikes, dvs 12:- eller två 1:a-klassgrundprisenheter. Tyngre brev kan kosta mer än dubbelt så mycket, särskilt utanför Europa.

När jag skulle skicka julkort till England denna jul blev jag positivt överraskad av att posten sålde 5 tolvkronorsfrimärken och 5 prioritaire-etiketter tillsammans i ett litet skicka-utrikes-kit. Något jag inte blev positivt överraskad av var att korten jag skickade 14 december kom fram idag, 10 januari, fastän postens hemsida säger att det bara ska ta 3 vardagar. Frågan är om den långa utdelningstiden berodde på slumpen, julruschen, julledigheten eller det faktum att jag inte skrev någon avsändare. (AndyMc konstaterar att hastigheten, ca 0.5 m/s, är ungefär en tredjedel av normal gånghastighet. Räknar man landvägen blir det ungefär hälften av normal gånghastighet, så det kanske var så att en stackars brevbärare promenerat från Linköping till Cambridge, med 12 timmars gång och 12 timmars vila per dag.)

Dynamical Systems handlar om:
* Fixpunkter
* Stabilitet
* Periodiska banor
* Bifurkationer
* Kaos

Allt intressant i denna kurs kommer sammanfattas i detta inlägg.

Dynamiska system

Med ett dynamiskt system menar jag en samling variabler som förändras med tiden efter en bestämd regel. I denna kurs behandlar vi dynamiska system av två typer:
* Kontinuerliga, som beskrivs av x'(t) = f(x(t)).
* Diskreta, som beskrivs av x(n+1) = g(x(n)).

Ett tråkigt exempel på ett diskret dynamiskt system är obegränsad befolkningstillväxt: Om x(n) är populationen efter n år, fås ekvationen x(n+1) = k·x(n), där k är en konstant.

Den logistiska ekvationen x(n+1) = k·x(n)·(A - x(n)) är en modell för befolkningstillväxt när området bara kan upprätthålla en begränsad population.

Ett exempel på ett kontinuerligt dynamiskt system är hastigheten hos en fallande partikel med luftmotstånd: v'(t) = g - kv(t)^2/m.

Det klassiska exemplet på ett kontinuerligt system är en tyngd i en fjäder, som beskrivs av elongationen x(t) från jämviktsläget och hastigheten v(t). Ekvationerna lyder x'(t) = v(t), v'(t) = -k·x(t). Här är en bild:


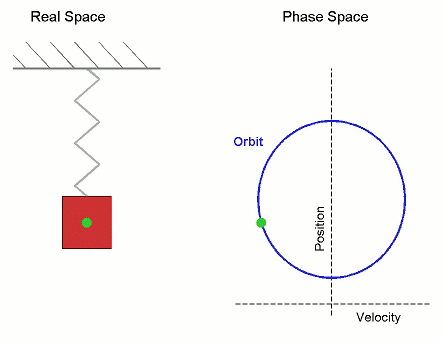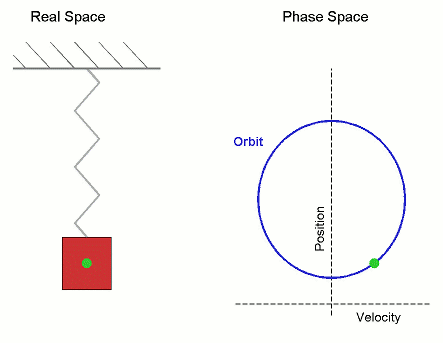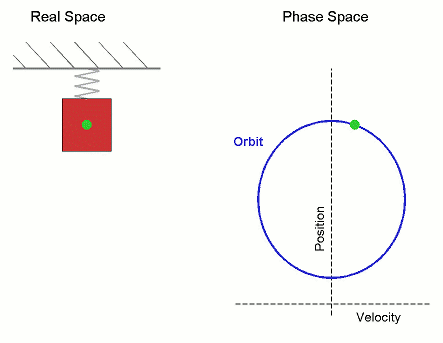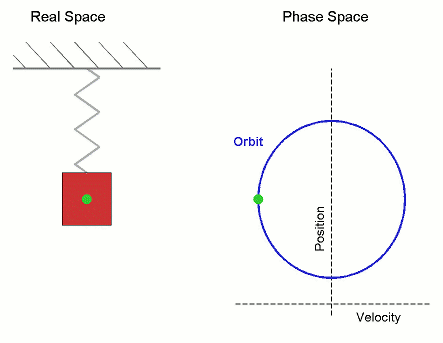
Fasrymden

Precis som den högra delen av ovanstående bild visar, tänker vi oss att variablerna i det dynamiska systemet är koordinater för en punkt i en lämplig rymd, fasrymden. I exemplet hade vi hastighet och position, som tolkas som x- och y-koordinat i planet. (Nu finner vi Wikipedias definition av ett dynamiskt system: En regel som beskriver hur en punkt i någon rymd förflyttas med tiden.)

I både det diskreta och det kontinuerliga fallet kan vi tala om banor (trajectories): Hur systemet utvecklas från en viss punkt. I det kontinuerliga fallet är detta en kurva i fasrymden (såsom cirkeln ovan), medan det i det diskreta fallet blir en sekvens av punkter.

Huvudpoängen i denna kurs är att bilda sig uppfattningar om hur banorna ser ut i fasrymden.

Den stora skillnaden på fasrymden och vanliga rymden, är att positionen i fasrymden fullständigt beskriver systemets tillstånd: För att beskriva en partikel i 3 dimensioner använder vi en sexdimensionell fasrymd - tre dimensioner för positionen, och tre för hastigheten.

Att systemet är fullständigt bestämt utifrån punktens position ger en viktig regel: Trajectories do not cross!. Om två banor möts i en punkt, så måste de fortsätta tillsammans, eftersom de följer exakt samma utvecklingsregler från denna punkt. I det kontinuerliga fallet kan man vanligtvis även köra systemet baklänges, så man kan rita fullständiga banor både framåt och bakåt i tiden från en given punkt. I det diskreta fallet är det vanligt att olika banor möts och fortsätter tillsammans, så när man spolar bandet baklänges blir det en massa förgreningar.

Regeln att banor inte korsas är viktig för kontinuerliga 2D-system, eftersom det begränsar möjligheterna drastiskt (till skillnad från i högre dimensioner där det är jättelätt att rita komplicerade figurer, exempelvis knutar, med kurvor som inte korsar varandra). Det är därför det krävs minst tre dimensioner för att ett kontinuerligt system ska kunna uppvisa kaotiskt beteende (se nedan).

Stabilitet

Den enklaste typen av bana är en fix punkt x₀. Den uppfyller
* f(x₀) = 0 för kontinuerliga system, så att x'(t) = 0.
* g(x₀) = x₀ för diskreta system, så att x(n+1) = x(n).

En intressant fråga är huruvida fixpunkten är stabil, dvs om systemet rubbas litegrann och istället följer banan x(t) = x₀ + δ(t), där δ(t) är litet till att börja med, hur kommer det då utveckla sig? Det visar sig (genom Taylorutveckling) att perturbationen δ(t) oftast ökar eller minskar exponentiellt, motsvarande att punkten är instabil eller stabil.

En annan sorts bana är periodiska banor (dvs banor som upprepar sig), exempelvis den som systemet i bilden ovan följer. Här kan man också analysera stabilitet.

Stabilitet är en viktig fråga, eftersom det är främst de stabila tillstånden man finner i den verkliga världen. Exempelvis är det en försvinnande liten andel av alla pennor i världen som just nu balanserar på sin spets.

Kaos

Kaos är idén att en fjärils vingslag kan orsaka en orkan på andra sidan jordklotet.

Denna idé är relaterad till det första kriteriet i definitionen av ett kaotiskt system: Sensitive dependence on initial conditions (SDIC). Detta innebär att små skillnader i utgångspunkt (exempelvis en fjärils vingslag) för det dynamiska systemet kan växa till jättestora skillnader (exempelvis en orkan).

Ursprungligen upptäcktes kaotiska system när man försökte förutspå vädret med hjälp av datorberäkningar. Någon hade låtit en dator göra en längre beräkning, och när denne startade om beräkningen från mitten med hjälp av de delresultat datorn hade skrivit ut blev slutresultatet helt annorlunda. Det berodde på att de utskrivna delresultaten var avrundade, och vid omkörningen växte de små avrundningsfelen genom SDIC och "förstörde" beräkningen.

Det är "på grund av" kaos som vi idag inte kan förutspå vädret mer än ungefär en vecka framåt i tiden: Går man längre blir felen från vädermodellens och mätvärdenas inexakthet för stora.

Notera att kaos uppstår trots att systemet är helt deterministiskt, dvs att det inte finns någon slump inblandad. Att slutresultatet ser slumpmässigt ut beror just på SDIC: I början mäter vi på systemet och finner att det befinner sig någonstans i ett litet område (som inte är en enda punkt på grund av mätosäkerheten). När vi spolar tiden framåt växer detta område och sprider ut sig över hela fasrymden. Vart systemet faktiskt tar vägen förefaller slumpmässigt.

Det andra kriteriet för kaos är Topological Transitivity (TT), vilket betyder att vilka två områden man än tänker på så finns det en bana som går från den ena till den andra. Detta utesluter tråkiga SDIC-system, såsom simpel exponentiell tillväxt (där det är uppenbart att små skillnader växer sig stora).

De två kriterierna för kaos kan alltså sammanfattas som "små skillnader kan explodera" och "banor blandas om". Ett exempel på ett kaotiskt system är dubbelpendeln: En pendel som det sitter en pendel på. Wikipedia har en bild på systemet:

och en exempelkörning (fast inte i den fyrdimensionella fasrymden, utan bara den tvådimensionella positionsrymden):


Att skriva om differentialekvationer till önskad form

Längst upp i detta inlägg definierade jag kontinuerliga system som x'(t) = f(x(t)), vilket är ett autonomt system av differentialekvationer av första ordningen. Det visar sig att många fler differentialekvationer kan skrivas på denna form, med hjälp av två trick.

Ett av dem har vi redan sett, nämligen hur man minskar ordningen av en ekvation genom att införa fler variabler. (Detta är användbart för MATLAB-användare, då MATLAB endast löser första ordningens diffekvationer.) Som jag nämnt i tidigare inlägg beskrivs ju fysiken för en partikel vanligtvis genom en andra ordningens diffekvation x''(t) = F(x'(t), x(t)). Genom att införa hastigheten v(t) = x'(t) som egen variabel blir den nya obekanta en tvådimensionell vektor (x(t), v(t)) som uppfyller diffekvationssystemet (x'(t), v'(t)) = f(x(t), v(t)) = (v(t), F(v(t), x(t))). Generellt, för att minska med k ordningar så behövs k nya variabler.

Det andra tricket är att omvandla ett icke-autonomt system (där regeln förändras med tiden) till ett autonomt system (där regeln inte beror på tiden), vilket exempelvis är användbart om man studerar sin pendel ombord på ett kapsejsande skepp. Detta löses genom att man inför tiden som egen variabel, T(t) = t. Istället för x'(t) = F(x(t), t) blir det (x'(t), T'(t)) = f(x(t), T(t)) = (F(x(t), T(t)), 1).

Andra exempel (bonuskapitel)

Pendel (på stång): Denna pendels position kan beskrivas med vinkeln mot lodlinjen, och som hastighet tar vi då tidsderivatan av vinkeln. Eftersom 0° rotation är samma som 360° rotation, blir fasrymden inte ett plan, utan en cylinder: Om man går 360° i positionsriktningen kommer man tillbaks till där man startade, men man kan gå godtyckligt långt i hastighetsriktningen utan att komma tillbaks (alla hastigheter är genuint olika).

Banorna ser ut såhär:

Bilden ska rullas ihop vertikalt, så att vänstra och högra kanten klistras ihop. I mitten finns vanliga oscillationer (libration), runt en stabil fixpunkt. Den fixpunkt som befinner sig längst till både höger och vänster i mitten är den där pendeln befinner sig rakt ovanför axeln, vilket självklart är instabilt. Längst uppe och nere är de tillstånd då pendeln har så hög fart att den bara snurrar runt åt ena hållet (rotation). De rödmarkerade banorna kallas separatriser, och är gränsen mellan libration och rotation. Där har pendeln lika mycket total energi som i den instabila fixpunkten, och systemet behöver oändlig tid på sig att nå denna punkt längs separatrisen.

Pendeln är ett specialfall av en generell klass av 2D-system kallade Hamiltonska system. Dessa kännetecknas av att man kan definiera en Hamiltonian H(x,y) (som måste uppfylla x' = dH/dy, y' = -dH/dx). Hamiltonianen tolkas som totala energin i systemet, eftersom det är just vad det är för exempelvis tyngden i fjädern ovan. (Mer om detta i CD).

Eftersom systemet följer banor med konstant Hamiltonian, blir det mycket lätt att analysera. Det är bara att rita nivåkurvorna (H = konstant) för Hamiltonianen, så har man systemets banor.

En lite svårare, men ändå relativt lätt, klass av system är nästan-Hamiltonska system. Detta är system som skiljer sig väldigt lite från Hamiltonska flöden, och analyseras genom att man studerar hur Hamiltonianen (för det snarlika Hamiltonska systemet) förändras längs banorna i detta nya system.

Exempelvis kan vi ta pendeln ovan, fast med någon sorts dämpning, säg luftmotstånd, i enkel svängning (libration). Utan luftmotstånd hade den svängt så för evigt, men nu förlorar den långsamt energi. Att lösa diffekvationssystemet fullständigt skulle vara svårt, men när luftmotståndet är svagt gör vi en approximation som följer: Vi antar att pendeln under en svängning följer den friktionsfria banan, men räknar ut hur mycket energi den skulle förlora om det fanns luftmotstånd. När svängningen är klar drar vi av denna energi, och räknar på nästa svängning på den nya, lägre, energinivån.

Denna metod kommer ge ett litet fel, eftersom pendeln egentligen saktar in kontinuerligt. Under varje svängning överskattar vi pendelns hastighet (och därmed luftmotståndet) när vi säger att den följer den friktionsfria banan genom fasrymden, så denna approximation ger antagligen en för snabb inbromsning (om inte andra faktorer spelar in). Felet är dock litet om luftmotståndet är litet.

Idag köpte jag byxor på Dressmann. Faktum är att jag köper i princip alla mina kläder (förutom T-shirts) på Dressmann.

Byxorna på Dressmann mäts i en tvådimensionell byxstorlek bestående av waist (omkrets kring midjan i tum, dvs någon sorts breddmått) och inseam (avstånd från skrev till anklar i tum, dvs någon sorts längdmått). Tydligen gör man så för jeans.

(Tvådimensionella klädstorlekar för icke-skräddarsydda kläder är för övrigt ingen nyhet, vilket alla kvinnor känner till: På bysthållare mäter man kupstorlek och omkrets under bysten, och det är också ekvivalent med att mäta omkrets runt och under bysten.)

Jag blev extra imponerad idag för att de hade sorterat byxorna i storleksordning. Exempelvis låg de mörkblå McGordon-jeansen fördelade på tre hyllor ovanför varandra, i fem högar på varje hylla. I den första högen låg alla jeans med midja 30, sorterade i insöm-ordning från den kortaste överst till den längsta underst; i nästa hög låg jeansen med midja 32; etc.

För drygt ett och ett halvt år sedan uppgraderade Corren sin hemsida, och de genomförde det riktigt dåligt. Till exempel hade de inte testat den nya sidan tillräckligt, så en mängd funktioner, bland annat söken, fungerade inte.

Jag var en flitig correnforumläsare på den tiden, och något som många forumanvändare blev sura över var att ingen hade förvarnats om att forumet också skulle uppgraderas utan att gamla inlägg fördes över. Över en natt försvann alla inlägg, för alltid. (Några klagade och bad Corren lägga upp de gamla arkiven så man kunde spara ner det man ville bevara, men detta hörsammades inte. Jag skulle gissa att anledningen var att det inte fanns några arkiv sparade.)

I det nya forumsystemet fanns precis som tidigare en massa underforum, såsom "Sport", "Kultur & nöje", etc. En nyhet var dock att man kunde kommentera direkt på nyhetsartiklar, vilket löstes tekniskt genom att artiklarna länkades samman med trådar i det nya underforumet "artikelkommentarer". Det var ingen högoddsare att detta underforum skulle få flest trådar - redan tidigare skapades de flesta trådar som reaktion på nyhetsartiklar - och idag ligger 92% av trådarna i detta forum.

Det var heller ingen högoddsare att det en dag skulle finnas så många trådar i ett underforum att de inte kunde visas på en enda sida. Det tänkte dock inte Correns programmerare på, och det var först efter (IIRC) 2000 artikelkommentartrådar och sex månader som sidvisning implementerades.

Ett tag hade de också ett intressant problem med foruminloggningen: Båda domänerna www.corren.se och corren.se gick att använda, men länkar till inloggningssidan från artiklar på corren.se gick till www.corren.se:s inloggning. Sedan när man loggat in på www.corren.se skickades man tillbaka till artikeln på corren.se, och möttes återigen av meddelandet att man inte var inloggad (på corren.se)! Nu har de dock ordnat så att allt på corren.se redirectar till www.corren.se (men inte nödvändigtvis till rätt ställe...).

Något som de ännu inte har fixat är den planerade rutan under varje artikel. Om man tittar i källkoden ser man att det finns en dold ruta med texten "(denna del har inte designats klart)" (tydligen är det inte bara Corren som har använt sig av dessa programmerare), och den har funnits där sedan uppgraderingen. Man kan visa denna ruta (och alla andra dolda) genom att skriva in denna kodsnutt i adressraden och trycka på enter:

javascript:if(a=document.getElementsByTagName('div'))for(i in a)if(a[i].style.display='block');

Då ser man att Correns programmerare har svårt att få pli på någon/några av följande funktioner: förminskar/förstora text, facebook-integration, utskriftsversion, tipsa en vän, debattera här, och publicerings-/uppdateringsdatum. (För övrigt är denna ruta det enda ställe där artikelns datum anges, även om publiceringsklockslaget står överst.)

(Anledningen till att jag skriver detta inlägg är att den där kodsnutten har suttit i en textfil på mitt skrivbord sedan 6 maj 2009, och jag vill ta bort filen utan att bli av med snutten.)

EDIT: Ytterligare en dålig sak är att artiklarna reloadar var 30.5:e minut. Man bör alltså inte sitta och komponera en lång kommentar i kommentarsfältet, om man inte känner för att plötsligt förlora allt. Man kan inte heller förvänta sig att fortsätta läsa artiklarna om man kopplar ner sig från internet, och man ska vara beredd på att få felmeddelanden när man väcker datorn ur sleep/hibernation eftersom sidan försöker laddas om direkt, innan nätverket har kommit igång.

Här är en lista på svengelska grundämnesnamn, närmare bestämt försvenskningar av de engelska namnen. Fet stil betyder att jag sett denna form i svensk text (vilket oftast innebär att författaren försökt snofsa till det eller har använt engelska källor).

Hydrogen, Lithium, Boron, Karbon, Nitrogen, Oxygen, Fluorin, Sodium, Silikon, Fosforus, Sulfur, Klorin, Potassium, Titanium, Vanadium, Kromium, Manganes, Selenium, Bromin, Niobium, Molybdenum, Tellurium, Jodin, Lantanum, Praseodymium, Neodymium, Tantalum, Tungsten, Platinum, Astatin, Thorium, Uranium.